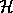We start our discussion on quite a general and somewhat abstract
level. Only later on, in examples, we will specialize
both: our system and the monitoring device.
We consider quantum system described using a Hilbert
space 
.
To answer the question "time of what?",
we must select a property of the system that we are going
to monitor. It must give only "yes-no", or one-zero answers.
We denote this binary variable with the letter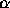 
. In our
case, starting at t=0,
when the monitoring begins, we will get continuously 
reading
on the scale,
until at a certain time, say 
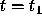, the reading will change into "yes".
Our aim is to get the statistics of these "first hitting times",
and to find out its dependence of the initial state of
the system and on its dynamics.
Speaking of the "time of events" one can also think that
"events" are transitions which occur; sometimes the system
is changing its state randomly - and these changes are
registered. There are two kinds of probabilities in
Quantum Mechanics the transition probabilities and
other probabilities - those that tell us when the
transitions occur. It is this second kind of probabilities
that we will discuss now.