

Next: Justification of the
Up: Time of Events
Previous: Second Postulate -
As noticed above in general we expect 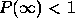 . That means
that if the experiment is repeated many times, then there will be
particles that were not registered while close to the counter;
they moved away, and they will never be registered in the future.
The natural question then arises: is the very presence of the
counter reflected in the dynamics of the particles that pass
the detector without being observed? Or we can put it as a
"quantum espionage" question: can a particle detect a detector
without being detected? And if so - which are the precise
equations that tell us how?.
. That means
that if the experiment is repeated many times, then there will be
particles that were not registered while close to the counter;
they moved away, and they will never be registered in the future.
The natural question then arises: is the very presence of the
counter reflected in the dynamics of the particles that pass
the detector without being observed? Or we can put it as a
"quantum espionage" question: can a particle detect a detector
without being detected? And if so - which are the precise
equations that tell us how?.
To answer this question it is not enough to use the two postulates
above. One needs to make use of the Event Engine of EEQT once more.
Our third postulate reads:
prior to any event, and independently of whether any event will
happen or not, the state of the system is described by the vector
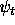 undergoing the non unitary
evolution given by Eq. (2). It is not too
difficult to think of an experiment that will test this
prediction.
undergoing the non unitary
evolution given by Eq. (2). It is not too
difficult to think of an experiment that will test this
prediction.
Fig. 1 shows four shots from time evolution of a
gaussian wavepacket monitored by a gaussian detector placed
at the center of the plane. The efficiency of the detector is
in this case ca. 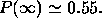 There is almost no
reflection. The shadow of the detector that is seen on the
fourth shot can be easily interpreted in terms of ensemble
interpretation: once we count only those particles that were
not registered by the detector, then it is clear that
there is nothing or almost nothing behind the detector.
However a careful observer will notice that there is
a local maximum exactly behind the counter. This is
a quantum effect, that of "interference of alternatives".
It has consequences for the rate of future events for
an individual particle.
There is almost no
reflection. The shadow of the detector that is seen on the
fourth shot can be easily interpreted in terms of ensemble
interpretation: once we count only those particles that were
not registered by the detector, then it is clear that
there is nothing or almost nothing behind the detector.
However a careful observer will notice that there is
a local maximum exactly behind the counter. This is
a quantum effect, that of "interference of alternatives".
It has consequences for the rate of future events for
an individual particle.


Next: Justification of the
Up: Time of Events
Previous: Second Postulate -
Arkadiusz Jadczyk
Thu Feb 22 09:58:31 MET 1996
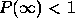 . That means
that if the experiment is repeated many times, then there will be
particles that were not registered while close to the counter;
they moved away, and they will never be registered in the future.
The natural question then arises: is the very presence of the
counter reflected in the dynamics of the particles that pass
the detector without being observed? Or we can put it as a
"quantum espionage" question: can a particle detect a detector
without being detected? And if so - which are the precise
equations that tell us how?.
. That means
that if the experiment is repeated many times, then there will be
particles that were not registered while close to the counter;
they moved away, and they will never be registered in the future.
The natural question then arises: is the very presence of the
counter reflected in the dynamics of the particles that pass
the detector without being observed? Or we can put it as a
"quantum espionage" question: can a particle detect a detector
without being detected? And if so - which are the precise
equations that tell us how?.


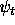 undergoing the non unitary
evolution given by Eq. (
undergoing the non unitary
evolution given by Eq. (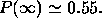 There is almost no
reflection. The shadow of the detector that is seen on the
fourth shot can be easily interpreted in terms of ensemble
interpretation: once we count only those particles that were
not registered by the detector, then it is clear that
there is nothing or almost nothing behind the detector.
However a careful observer will notice that there is
a local maximum exactly behind the counter. This is
a quantum effect, that of "interference of alternatives".
It has consequences for the rate of future events for
an individual particle.
There is almost no
reflection. The shadow of the detector that is seen on the
fourth shot can be easily interpreted in terms of ensemble
interpretation: once we count only those particles that were
not registered by the detector, then it is clear that
there is nothing or almost nothing behind the detector.
However a careful observer will notice that there is
a local maximum exactly behind the counter. This is
a quantum effect, that of "interference of alternatives".
It has consequences for the rate of future events for
an individual particle.