

Next: Second Postulate -
Up: Time of Events
Previous: Time of Events
Our first postulate reads: the coupling to a "yes-no"
monitoring device is described by an operator
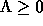 in the Hilbert space
in the Hilbert space 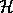 .
In general
.
In general 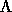 may explicitly
depend on time but here, for simplicity, we will assume that
this is not the case. That means: to any real experimental
device there corresponds a
may explicitly
depend on time but here, for simplicity, we will assume that
this is not the case. That means: to any real experimental
device there corresponds a 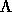 . In practice it may be
difficult to produce the
. In practice it may be
difficult to produce the  that describes exactly
a given device. As it is difficult to find the Hamiltonian
that takes into account exactly all the forces that
act in a system. Nevertheless we believe that an exact
Hamiltonian exists, even if it is hard to find or impractical
to apply. Similarly our postulate states that an exact
that describes exactly
a given device. As it is difficult to find the Hamiltonian
that takes into account exactly all the forces that
act in a system. Nevertheless we believe that an exact
Hamiltonian exists, even if it is hard to find or impractical
to apply. Similarly our postulate states that an exact 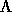 exists, although it may be hard to find or impractical
to apply. Then we use an approximate one, a model one.
exists, although it may be hard to find or impractical
to apply. Then we use an approximate one, a model one.
It should be noticed that we do not assume that 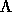 is an orthogonal projection. This reflects the fact that our
device - although giving definite "yes-no" answers,
gives them acting upon possibly fuzzy criteria. In the
limit when the criteria become sharp one should think
of
is an orthogonal projection. This reflects the fact that our
device - although giving definite "yes-no" answers,
gives them acting upon possibly fuzzy criteria. In the
limit when the criteria become sharp one should think
of 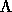 as
as 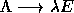 , where
, where
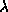 is a coupling constant of physical dimension
is a coupling constant of physical dimension
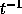 and E a projection operator. In the general case
it is usually convenient to write
and E a projection operator. In the general case
it is usually convenient to write 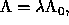 where
where 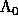 is dimensionless.
is dimensionless.
It is also important to notice that the property that is being
monitored by the device
need not be an elementary one. Using the concepts
of quantum logic (cf. [18,19]) the property need not
be atomic -
it can be a composite property. In such a case,
when thinking about physical implementation of the procedure
determining whether the property holds or no, there are two
extreme cases. Roughly speaking the situation here is similar to
that occurring in discussion of superpositions of state preparation
procedures. Some procedures lead to a coherent superpositions,
some other lead to mixtures. Similarly with composite detectors:
one possibility is that we have
a distributed array of detectors that can act independently of each
other, and our event consists
on activating one of them. Another possibility is
that we have a coherent distributed detector like a
solid state lattice that acts as one detector.
In the first case (called incoherent) 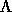 will
be of the form
will
be of the form

while in the second coherent case:
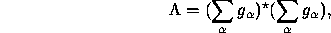
where 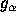 are operators associated to individual
constituents of the detector's array. More can be said
about this important topic, but we will not need to
analyze it in more details for the present purpose.
are operators associated to individual
constituents of the detector's array. More can be said
about this important topic, but we will not need to
analyze it in more details for the present purpose.


Next: Second Postulate -
Up: Time of Events
Previous: Time of Events
Arkadiusz Jadczyk
Thu Feb 22 09:58:31 MET 1996
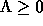 in the Hilbert space
in the Hilbert space 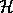 .
In general
.
In general 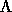 may explicitly
depend on time but here, for simplicity, we will assume that
this is not the case. That means: to any real experimental
device there corresponds a
may explicitly
depend on time but here, for simplicity, we will assume that
this is not the case. That means: to any real experimental
device there corresponds a 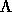 . In practice it may be
difficult to produce the
. In practice it may be
difficult to produce the  that describes exactly
a given device. As it is difficult to find the Hamiltonian
that takes into account exactly all the forces that
act in a system. Nevertheless we believe that an exact
Hamiltonian exists, even if it is hard to find or impractical
to apply. Similarly our postulate states that an exact
that describes exactly
a given device. As it is difficult to find the Hamiltonian
that takes into account exactly all the forces that
act in a system. Nevertheless we believe that an exact
Hamiltonian exists, even if it is hard to find or impractical
to apply. Similarly our postulate states that an exact  exists, although it may be hard to find or impractical
to apply. Then we use an approximate one, a model one.
exists, although it may be hard to find or impractical
to apply. Then we use an approximate one, a model one.

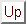

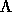 is an orthogonal projection. This reflects the fact that our
device - although giving definite "yes-no" answers,
gives them acting upon possibly fuzzy criteria. In the
limit when the criteria become sharp one should think
of
is an orthogonal projection. This reflects the fact that our
device - although giving definite "yes-no" answers,
gives them acting upon possibly fuzzy criteria. In the
limit when the criteria become sharp one should think
of 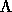 as
as 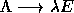 , where
, where
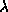 is a coupling constant of physical dimension
is a coupling constant of physical dimension
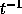 and E a projection operator. In the general case
it is usually convenient to write
and E a projection operator. In the general case
it is usually convenient to write 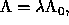 where
where 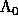 is dimensionless.
is dimensionless.
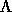 will
be of the form
will
be of the form

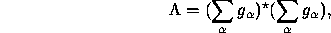
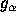 are operators associated to individual
constituents of the detector's array. More can be said
about this important topic, but we will not need to
analyze it in more details for the present purpose.
are operators associated to individual
constituents of the detector's array. More can be said
about this important topic, but we will not need to
analyze it in more details for the present purpose.