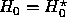 . We denote by
. We denote by
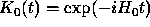 the corresponding unitary propagator.
Again, for simplicity, we will assume that
the corresponding unitary propagator.
Again, for simplicity, we will assume that 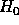 does not
depend explicitly on time.
does not
depend explicitly on time.

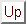

We assume that, apart of the monitoring device, our system
evolves under time evolution described by the Schrödinger
equation with a self--adjoint Hamiltonian 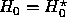 . We denote by
. We denote by
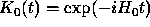 the corresponding unitary propagator.
Again, for simplicity, we will assume that
the corresponding unitary propagator.
Again, for simplicity, we will assume that 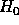 does not
depend explicitly on time.
does not
depend explicitly on time.
Our second postulate reads: assuming that the monitoring
started at time t=0, when the system was described
by a Hilbert space vector 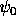 ,
, 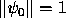 ,
and when the monitoring
device was recording the logical value "no", the
probability
,
and when the monitoring
device was recording the logical value "no", the
probability 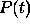 that the change
that the change 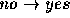 will
happen before time t is given by the formula:
will
happen before time t is given by the formula:
where
and
Remark: The factor  in the formula above is put
here for consistency with the notation used in our previous
papers.
in the formula above is put
here for consistency with the notation used in our previous
papers.
It follows from the formula (1) that the probability
that the counter will be triggered out in the time interval (t,t+dt),
provided it was not triggered yet, is 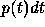 , where
, where 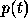 is
given by
is
given by
We remark that 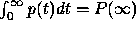 is the probability that
the detector will notice the particle at all. In general this number
representing the total efficiency of the detector (for a given initial
state) will be smaller than
is the probability that
the detector will notice the particle at all. In general this number
representing the total efficiency of the detector (for a given initial
state) will be smaller than