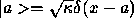 ,
placed at x=a, to a Gaussian wave packet whose initial shape
at t=0 is given by:
,
placed at x=a, to a Gaussian wave packet whose initial shape
at t=0 is given by:

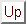

We consider now another example corresponding to a free Schrödinger's particle on a line.
We will study response of a Dirac's delta counter 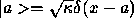 ,
placed at x=a, to a Gaussian wave packet whose initial shape
at t=0 is given by:
,
placed at x=a, to a Gaussian wave packet whose initial shape
at t=0 is given by:
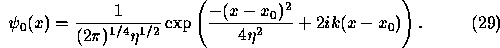
In the following it will be convenient to use dimensionless variables for measuring space, time and the strength of the coupling:
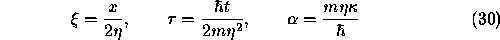
We denote
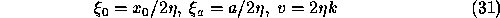
In these new variables we have:
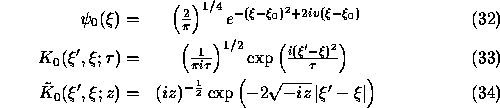
We can compute now explicitly 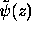 of
Eq. (13):
of
Eq. (13):
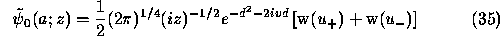
where
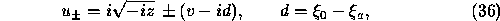
and the amplitude 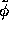 of Eq. (26), when rendered
dimensionless,
of Eq. (26), when rendered
dimensionless, reads
reads
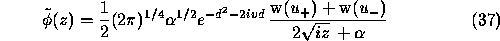
with the function 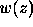 defined by
defined by
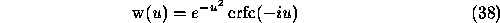
(see Ref. [30], Ch. 7.1.1 -- 7.1.2). We have also used the formula
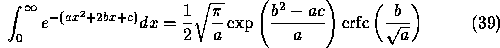
valid for 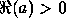 (see [30], Ch. 7.4.2).
(see [30], Ch. 7.4.2).
To compute 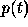 from Eqs. (20,21) the correct boundary values
of the complex square root (with the cut on the negative real half-axis)
must be taken. Thus for
from Eqs. (20,21) the correct boundary values
of the complex square root (with the cut on the negative real half-axis)
must be taken. Thus for 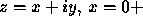 we should take
we should take
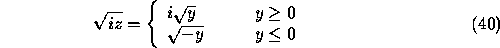
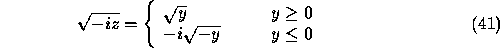
The time of arrival probability curves of the counter for several values of
the coupling constant are shown in Fig.2. The incoming wave packet starts at
t=0, x=-4, with velocity 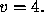 It is seen from the plot that the average
time at which the counter, placed at x=0, is triggered is about
one time unit, independently of the value of the coupling constant.
This numerical example shows that
our model of a counter serves can be used for measurements of time of
arrival. It is to be noticed that the shape of the response curve is
almost insensitive to the value of the coupling constant. Fig.3 shows
the curves of Fig.2, but rescaled in such a way that
the probability
It is seen from the plot that the average
time at which the counter, placed at x=0, is triggered is about
one time unit, independently of the value of the coupling constant.
This numerical example shows that
our model of a counter serves can be used for measurements of time of
arrival. It is to be noticed that the shape of the response curve is
almost insensitive to the value of the coupling constant. Fig.3 shows
the curves of Fig.2, but rescaled in such a way that
the probability 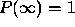 . The
only effect of the increase of the coupling constant in the interval
. The
only effect of the increase of the coupling constant in the interval
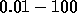 is a slight shift of the response time to the left - which
is intuitively clear. Notice that the shape of the curve in time corresponds
well to the shape of the initial wave packet in space.
is a slight shift of the response time to the left - which
is intuitively clear. Notice that the shape of the curve in time corresponds
well to the shape of the initial wave packet in space.
For a given velocity of the packet
there is an optimal value of the coupling constant. In our dimensionless
units it is 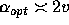 .
Figure 4 shows this asymptotically linear dependence. At the optimal
coupling the total response probability
.
Figure 4 shows this asymptotically linear dependence. At the optimal
coupling the total response probability 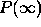 approaches the value
approaches the value 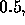 - the same as in the ultra--relativistic case.
- the same as in the ultra--relativistic case.
By numerical calculations we have found that the maximal value of 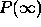 that can be obtained for a single Dirac's delta counter and Schrödinger's
particle is slightly higher than
that can be obtained for a single Dirac's delta counter and Schrödinger's
particle is slightly higher than 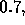 that corresponds to the value
that corresponds to the value
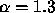 of
the coupling constant. The dependence of
of
the coupling constant. The dependence of 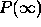 on the coupling constant
for a static wave packet (that is v=0) centered exactly over the detector is
shown in Fig.5.
Fig.6 shows the dependence of
on the coupling constant
for a static wave packet (that is v=0) centered exactly over the detector is
shown in Fig.5.
Fig.6 shows the dependence of 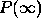 on both variables: v and
on both variables: v and 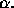
The value 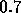 for the maximal response probability
for the maximal response probability 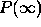 of a detector
may appear to be rather strange. It is however connected with the point--like
structure of the detector in our simple model. For a composite detector,
for instance already for a two--point detector, this restriction does not
apply and
of a detector
may appear to be rather strange. It is however connected with the point--like
structure of the detector in our simple model. For a composite detector,
for instance already for a two--point detector, this restriction does not
apply and 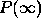 arbitrarily close to
arbitrarily close to 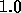 can be obtained.
Our method applies as well to detectors continuously distributed in space.
In this case the efficiency of the detector (for a given initial wavepacket)
will depend on the shape of
the function
can be obtained.
Our method applies as well to detectors continuously distributed in space.
In this case the efficiency of the detector (for a given initial wavepacket)
will depend on the shape of
the function 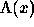 . The absorptive complex potentials studied in
[31,32] are natural candidates for providing maximal efficiency as
measured by
. The absorptive complex potentials studied in
[31,32] are natural candidates for providing maximal efficiency as
measured by 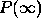 defined at the end of Sec. 2.2.
defined at the end of Sec. 2.2.