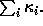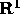 and that the Hilbert space vector |a> approaches the
improper position eigenvector
and that the Hilbert space vector |a> approaches the
improper position eigenvector 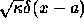 localized at the point a.
This corresponds to a point--like detector of strength
localized at the point a.
This corresponds to a point--like detector of strength  placed at a.
placed at a. We see from the
equation (4) that
We see from the
equation (4) that 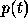 is in this case given by:
is in this case given by:

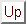

Let us now specialize the model by assuming that we consider a particle
in 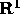 and that the Hilbert space vector |a> approaches the
improper position eigenvector
and that the Hilbert space vector |a> approaches the
improper position eigenvector 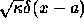 localized at the point a.
This corresponds to a point--like detector of strength
localized at the point a.
This corresponds to a point--like detector of strength  placed at a.
placed at a. We see from the
equation (4) that
We see from the
equation (4) that 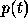 is in this case given by:
is in this case given by:
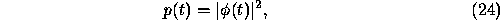
where the complex amplitude 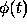 of the particle arriving at a is:
of the particle arriving at a is:
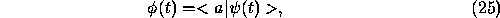
or, from Eq. (12)
where
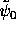 stands for the Laplace transform of
stands for the Laplace transform of 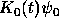 .
.
Let us now consider the simplest explicitly solvable example - that of an
ultra--relativistic particle on a line. For 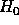 we take
we take 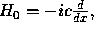 then the propagator
then the propagator 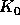 is given by
is given by 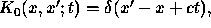 and its
Laplace transform reads
and its
Laplace transform reads 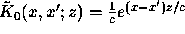 . In
particular
. In
particular 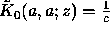 and from Eq. (26) we
see that the amplitude for arriving at the point a is given by the "almost
evident" formula:
and from Eq. (26) we
see that the amplitude for arriving at the point a is given by the "almost
evident" formula:
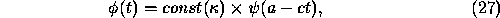
where
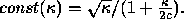 It follows that probability that the particle will be registered is equal to
It follows that probability that the particle will be registered is equal to
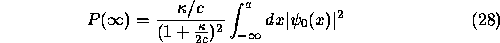
which has a maximum 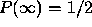 for
for 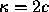 if the support of
if the support of 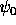 is left to the counter position
is left to the counter position 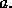 We notice that in this
example the
shape of the arrival time probability distribution
We notice that in this
example the
shape of the arrival time probability distribution 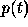 does not depend
on the value of the coupling constant - only the effectiveness of the
detector depends on it. For a counter corresponding to a superposition
does not depend
on the value of the coupling constant - only the effectiveness of the
detector depends on it. For a counter corresponding to a superposition
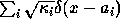 we obtain for
we obtain for 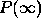 exactly the
same expression as for one counter but with
exactly the
same expression as for one counter but with  replaced with
replaced with