Our approach to the quantum mechanical measurement problem was
originally shaped to a large extent by the important paper by
Klaus Hepp [33].
He wrote there, in the concluding section: The solution of the
problem of measurement is closely connected with the yet unknown
correct description of irreversibility in quantum mechanics...
Our approach does not pretend to give an ultimate solution. But
it attempts to show that this "correct description" is, perhaps,
not too far away.
In the present paper we have only been able to scratch the surface of some
of the new mathematical
techniques and physical ideas that are enhancing quantum theory in the framework
of EEQT, that free the quantum theory from the limitations of the standard
formulation. For a long time it was considered that quantum theory is only
about averages. Its numerical predictions were supposed to come only
from expectation values of linear operators.
On the other hand in his 1973 paper [34]
Wigner wrote: It seems unlikely,
therefore, that the superposition principle applies in full force to
beings with consciousness. If it does not, or if the linearity of
the equations of motion should be invalid for systems in which life
plays a significant role, the determinants of such systems
may play the role which proponents of the hidden variable theories
attribute to such variables. All proofs of the unreasonable nature
of hidden variable theories are based on the linearity of the
equations ... .
Weinberg [35]
attempted to revive and to implement Wigner's idea of non-linear
quantum mechanics. He proposed a nonlinear framework and also
methods of testing for linearity. Warnings against potential dangers
of nonlinearity are well known, they were summarized in a recent paper
by Gisin and Rigo [36]. The scheme of EEQT avoids these pitfalls
and presents a consistent and coherent theory. It
introduces necessary nonlinearity in the algorithm for generating
sample histories of individual systems, but preserves linearity
on the ensemble level. It is not only about averages but also
about individual events (cf. the event generating PDP algorithm of ref.
[6]). Thus it explains more, it predicts more and it opens
a new gateway leading beyond today's framework and towards new applications of
Quantum Theory. These new applications may involve the problems
of consciousness. But in our opinion (supported in the all quoted papers
on EEQT, and also in the present one) quantum theory does not need
neither consciousness nor human observers - at least not more
than any other probabilistic theory. On the other hand, to understand
mind and consciousness we may need Event Enhanced Quantum Theory. And more.
In the abstract to the present paper we stated that we "enhance elementary
quantum mechanics with three simple postulates". In fact the PDP
algorithm replaces the standard measurement postulates and enables
us to derive them in a refined form. This is because EEQT defines\
precisely what measurement and experiment is - without
any involvement of consciousness or of human observers. It is only
for the purpose of the present paper - to introduce time observable
into elementary quantum mechanics as simply as possible - that we
have chosen to present our three postulates as postulates rather
than theorems.
The time observable that we introduced
and investigated in the present paper is just one (but important)
trace of this nonlinearity.
Time of arrival, time of detector
response, is an "observable", is a random variable whose
probability distribution function can be computed according
to the prescription that we gave in the previous section. But
its probability distribution is not a bilinear functional of
the state and as a result "time of arrival" can not be represented
by a linear operator, be it Hermitian or not. Nevertheless
our "time" of arrival is a "safe" nonlinear observable. Its
safety follows from the fact that what we called "postulates"
in the present paper are in fact "theorems" of the general
scheme EEQT. And EEQT is the minimal extension of quantum
mechanics that accounts for events: no extra unnecessary
hidden variables, and linear Liouville equation for ensembles.
Our definition of time of arrival bears some similarity to
the one proposed long ago by Allcock [38].
Although we disagree in several important points with
the premises and conclusions of this paper, nevertheless
the detailed analysis of some aspects of the problem
given by Allcock was prompting us to formulate and to solve
it using the new perspective and the new tools that EEQT
endowed us with. Our approach to the problem of time of arrival
goes in a similar direction as
the one discussed in an (already quoted) interesting recent
paper by Muga and co--workers [32]. We share many of his views. The
difference being that what the authors of [32] call
"operational model" we promote to the role of a fundamental
new postulate of quantum theory. We justify it and point out that
it is a theorem of a more fundamental theory - EEQT.
Moreover we take the non--unitary evolution before the detection
event seriously and point out that the new theory is experimentally
falsifiable.
Once the time of arrival observable has been defined, it is
rather straightforward to apply it. In particular our time
observable solves Mielnik's "waiting screen problem"
[39]. But not only that; with our
precise definition at hand, one can approach again the old
puzzle of time--energy uncertainty relation in the spirit
of Wigner's analysis [40] (cf. also [41,42].
One can also approach
afresh the other old problem: that of decay times (see [43] and references therein) and of
tunneling times ([44,45,46] and
references therein).
This last problem needs however more than just one detector.
We need to analyse the joint distribution probability for two
separated detector. We must also know how to describe
the unavoidable disturbance of the wave function when
the first detector is being triggered. For this the
simple postulates of this paper do not suffice. But
the answer is in fact quite easy if using the event
generating algorithm of EEQT.
More investigations needs also our "shadowing
effect" of section 2.3. Every "real" detector acts
not only as an information exchange channel, but also
as an energy--momentum exchange channel. Every real
detector has not only its "information temperature"
described by our coupling constant 
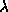(cf. Sec.
2.1), but also ordinary temperature. Experiments
to test the effect must take care in separating
these different contributions to the overall
phenomenon. This is not easy. But the theory is falsifiable
in the laboratory and critical experiments might
be feasible within the next couple of years.
In the introductory chapter the problem of
extension of the present framework to the
relativistic case has been shortly mentioned. Work
in this direction is well advanced and we
hope to be able to report its result soon. But
this will not be end of the story. At the very
least we have much to learn about the nature and the
mechanism of the coupling between Q and C.
Acknowledgements
One of us (A.J) acknowledges with thanks support of A. von Humboldt
Foundation. He also thanks Larry Horwitz for encouragement,
Rick Leavens for his interest and pointing out the relevance of
Muga's group papers and to Gonzalo Muga for critical comments.
We are indebted to Walter Schneider for his
interest, critical reading of the manuscript and for supplying
us with relevant informations. We thank Rudolph Haag for sending
us the first draft of [17].