

Next: About this document
Up: No Title
Previous: Concluding Remarks
References
- 1
- Galileo Galilei, "Dialogues
Concerning Two New Sciences, Dover Publ., New York 1954
- 2
- Blanchard, Ph. and Jadczyk, A.: Strongly coupled
quantum and classical systems and Zeno's effect,
Phys. Lett. A 183 (1993) 272--276, and references therein
- 3
- Zeh, H.D.: There are no quantum jumps nor there are
particles , Phys. Lett. A 172 (1993) 189--192
- 4
- Ballentine, L.E.: Limitation of the Projection Postulate
, Found. Phys 11 (1990) 1329--1343
- 5
- Ballentine, L.E.: Failure of Some Theories of State
Reduction , Phys. Rev. A 43 (1991) 9--12
- 6
- Blanchard, Ph., and A. Jadczyk.:
Event--Enhanced--Quantum Theory and Piecewise Deterministic Dynamics,
Ann. der Physik 4 (1995) 583--599,
hep-th 9409189; see also the short version: Event and Piecewise
Deterministic Dynamics in Event--Enhanced Quantum Theory , Phys.Lett.
A 203 (1995) 260--266
- 7
- Jadczyk, A.: Particle Tracks, Events and Quantum
Theory, Progr. Theor. Phys. 93 (1995) 631--646, hep-th/9407157
- 8
- Jadczyk, A.: On Quantum Jumps, Events and Spontaneous
Localization Models, Found. Phys. 25 (1995) 743--762,
hep-th/9408020
- 9
- Belavkin, V.P., Melsheimer, O.: A Hamiltonian
Approach to Quantum Collapse, State Diffusion and Spontaneous
Localization , in Quantum Communications and Measurement, Ed.
V.P. Belavkin et al, Plenum Press, New York 1995
- 10
- Mott, N.F.: The Wave Mechanics of
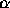 --Ray Tracks ,
Proc. Roy. Soc. A 125(1929) 79--884
--Ray Tracks ,
Proc. Roy. Soc. A 125(1929) 79--884
- 11
- Dicke, R.H.: Interaction--free quantum measurements: A paradox?
, Am. J. Phys 49 (1981) 925--930
- 12
- Dicke, R.H.: On Observing the Absence of an Atom , in
Between Quantum and Chaos, Ed. Zurek, W. et al., Princeton University
Press, Princeton 1988, pp. 400--407
- 13
- Elitzur, A., Vaidman, L.: Quantum Mechanical Interaction--Free
Measurements , Found. Phys 23 (1993)
987--997
- 14
- Kwiat, P., Weinfurter, H., Herzog, T, Zeilinger, A.:
Interaction--Free Measurement , Phys. Rev. Lett. 74 (1995) 4763--4766
- 15
- Unruh, W.G.: Particles and Fields in Quantum
Mechanics in Curved Space--Time, Ed. Audretsch et al, NATO ASI Series B 230,
Plenum Press, New York, 1990
- 16
- Bialynicki--Birula, I.: Is Time Sharp or Diffused ,
in Physical Origins of Time Asymmetry , Ed. Halliwell, J.J. et al.,
Cambridge University Press 1994
- 17
- Haag, R.: An evolutionary picture for Quantum Physics ,
to appear, 1996
- 18
- Jauch, J.M.: Foundations of Quantum Mechanics, Addison--Wesley,
Reading, Ma. 1968
- 19
- Piron, C.: Foundations of Quantum Physics, W.A. Benjamin,
London 1976
- 20
- Dattoli, G., Torre, A., Mignani, R.: Non--Hermitian
evolution of two--level quantum systems , Phys. Rev. A 42 (1990)
1467--1475
- 21
- Jost, R.: Bemerkungen zur mathematischen Theorie der Zähler
, Helv. Phys. Acta 20 (1947) 173--182
- 22
- Jadczyk, A., Kondrat, G., and Olkiewicz, R.: On
uniqueness of the jump process in quantum measurement theory,
Preprint BiBoS 711/12/95, quant-ph/9512002
- 23
- Bauch, D.: The Path Integral for a Particle
Moving in a
 -Function Potential , Nuovo Cim. 85 B
(1985) 118--123
-Function Potential , Nuovo Cim. 85 B
(1985) 118--123
- 24
- Gaveau, B., and Schulman, L.S.: Explicit time dependent
Schrödinger propagators , J. Phys. A 19 (1986) 1833--1846
- 25
- Blinder, S.M.: Green's function and propagator
for the one--dimensional
 --function potential , Phys. Rev.
A 37 (1987) 973--976
--function potential , Phys. Rev.
A 37 (1987) 973--976
- 26
- Lavande, S.V. and Bhagwat, K.V.: Feynman propagator
for the
 -function potential , Phys. Lett. A 131
(1988) 8--10
-function potential , Phys. Lett. A 131
(1988) 8--10
- 27
- Albeverio, S., Gesztesy, F., Høegh--Krohn, R., Holden,
H. Solvable Models in Quantum Mechanics, Springer, New York 1988,
- 28
- Manoukian, E.B.: Explicit derivation for a Dirac
 potential J. Phys. A 22 (1989) 67--70
potential J. Phys. A 22 (1989) 67--70
- 29
- Grosche, C.: Path integrals for potential problems with
 --function perturbation , J. Phys A 23 (1990) 5205--5234
--function perturbation , J. Phys A 23 (1990) 5205--5234
- 30
- Abramowitz, M., Stegun, I.: Handbook of Mathematical
Functions, Dover, New York 1972
- 31
- Brouard, S., Macias, D. and Muga, J.G.:
Perfect absorbers for stationary and wavepacket scattering ,
J. Phys. A 27 (1994) L439--L445
- 32
- Muga, J.G., Brouard, S., and Macias, D.: Time
of Arrival in Quantum Mechanics , Ann. Phys. 240
(1995) 351--366
- 33
- Hepp, K.: Quantum Theory of Measurement and
Macroscopic Observables , Helv. Phys. Acta 45 (1972)
237--248
- 34
- Wigner, E.P.: Epistemological Perspective on
Quantum Theory , in Contemporary Research in the Foundations and
Philosophy of Quantum Theory , Hooker (ed.), Reidel Publ. Comp.,
Dordrecht 1973
- 35
- Weinberg, S.: Testing Quantum Mechanics ,
Ann. Phys. 194 (1989) 336--386
- 36
- Gisin, N., Rigo, M.: Relevant and irrelevant nonlinear
Schrödinger equations , J. Phys. A 28 (1995) 7375--7390
- 37
- Kijowski, J.: On the time operator in
quantum mechanics and the
Heisenberg uncertainty relation for energy and time , Rep. Math. Phys.
6 (1974) 361--386
- 38
- Allcock, G.R.:
The Time Arrival in Quantum Mechanics: I. Formal
Considerations , Ann. Phys. 53 (1969) 252--285
- 39
- Mielnik, B.: The Screen Problem , Found. Phys.
24 (1994) 1113--1129
- 40
- Wigner, E.P.: On the Time--Energy Uncertainty Relation
, in Aspects of Quantum Theory, Ed. Salam, E., and Wigner, E.P. ,
Cambridge University Press, Cambridge 1972
- 41
- Recami, E.:
A Time Operator and the Time--Energy Uncertainty
Relation , in The Uncertainty Principle and Foundations
of Quantum Mechanics, Ed. Price, W.C. et al., Wiley, London 1977
- 42
- Pfeifer, P., and Fröhlich, J.: Generalized
Time--Energy Uncertainty Relations and Bounds on Life Times
Resonances , Preprint ETH-TH/94-31
- 43
- Eisenberg, E., and Horwitz, L.P.:
Time, Irreversibility and Unstable Systems in Quantum Physics ,
Adv. Chem. Phys., to appear
- 44
- Olkhowsky, V.S., and Recami, E.: Recent Developments in the
Time Analysis of Tunelling Processes , Phys. Rep. 214 (1992) 339--356
- 45
- Landauer, R.: Barrier interaction time in tunneling ,
Rev. Mod. Phys. 66 (1994) 217--228
- 46
- Leavens, C.R.: The "tunneling time problem": fundamental
incompatibility of the Bohm trajectory approach with the projector and
conventional probability current approaches , Phys. Lett.
A 197 (1995) 88--94
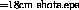
Figure 1: Four shots from the time evolution of a
gaussian wavepacket monitored by a gaussian detector placed
at the center of the plane. The efficiency of the detector is
in this case ca. 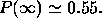

Figure 2: Probability density of time of arrival for a Dirac's delta counter
placed at x=0, coupling constant alpha. The incoming wave packet starts at t=0,
x=-4, with velocity v=4

Figure 3: Rescaled probability densities of Fig.1

Figure 4: Optimal coupling constant as a function of velocity of the incoming
wave packet. The dependence pretty soon saturates to a linear one. At the
saturation value 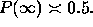

Figure 5: 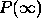 as a function of
as a function of 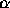 for a static wave packet
centered over the counter. The maximum, of
for a static wave packet
centered over the counter. The maximum, of 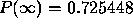 is reached
for
is reached
for 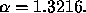

Figure 6: 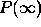 as a function of velocity v and coupling constant
as a function of velocity v and coupling constant 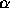 for
a static wave packet centered over the detector.
for
a static wave packet centered over the detector.
47 Greenstein, G., Zajonc, A.G.: Do Quantum
Jumps Occur at Well Defined Moments of Time? ,
Am. J. Phys. 63 (1995) 743--745
48 Kärtner, F.X., Haus, H.A.: Quantum--nondemolition
measurements and the "collapse of the wave function , Phys. Rev
A 47 (1993) 4585--4592
49 Zeh, H.D.: Decoherence and Quantum Measurements ,
in Stochastic Evolution of Quantum Systems in Open Systems and
in Measurement Processes, Ed. L. Diosi and B. Lukacs, World Scientific,
Singapore 1994
50 Broyles, A.A.: Nature of Quantum Jumps ,
Phys. Rev. A 45 (1992) 4925--4931
51 Blanchard, Ph. and Jadczyk, A.:
Quantum Mechanics with Event Dynamics, Rep. Math. Phys. 36
No 2/3 (1995), to appear
quant-ph/9506014,
Arkadiusz Jadczyk
Thu Feb 22 09:58:31 MET 1996
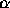 --Ray Tracks ,
Proc. Roy. Soc. A 125(1929) 79--884
--Ray Tracks ,
Proc. Roy. Soc. A 125(1929) 79--884
 -Function Potential , Nuovo Cim. 85 B
(1985) 118--123
-Function Potential , Nuovo Cim. 85 B
(1985) 118--123
 --function potential , Phys. Rev.
A 37 (1987) 973--976
--function potential , Phys. Rev.
A 37 (1987) 973--976
 -function potential , Phys. Lett. A 131
(1988) 8--10
-function potential , Phys. Lett. A 131
(1988) 8--10
 potential J. Phys. A 22 (1989) 67--70
potential J. Phys. A 22 (1989) 67--70
 --function perturbation , J. Phys A 23 (1990) 5205--5234
--function perturbation , J. Phys A 23 (1990) 5205--5234


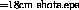
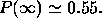



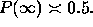

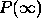 as a function of
as a function of 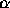 for a static wave packet
centered over the counter. The maximum, of
for a static wave packet
centered over the counter. The maximum, of 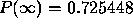 is reached
for
is reached
for 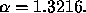

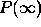 as a function of velocity v and coupling constant
as a function of velocity v and coupling constant 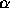 for
a static wave packet centered over the detector.
for
a static wave packet centered over the detector.