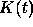Let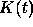 
be given by Eq. (3), and let
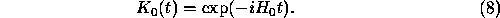
Then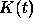 
satisfies the Schrödinger equation
This differential equation, together with initial data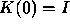 
, is easily seen to be
equivalent to the following integral equation:
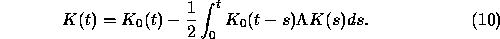
By taking the Laplace transform and by the convolution theorem we get the Laplace transformed equation:
Let us consider the case of a maximally sharp measurement. In this case
we would take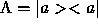 
, where |a> is some Hilbert space vector.
It is not assumed
to be normalized; in fact its norm stands for the strength of the coupling
(notice that <a|a> must have physical dimension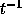 
).
Taking look at the formula (4)
we see that now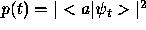 
and so we need to know
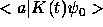rather than the full propagator 
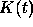. Multiplying Eq. (11)
from the left by <a| and from the right by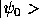 
we obtain:
where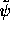 
is the Laplace transform of 
:
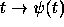