

Event Enhanced Quantum Physics (EEQT)
Links to my other online papers dealing with hyperdimensional physics
EEQT, Quantum Jumps and Quantum FractalsPaper "Quantum Jumps, EEQT and the Five Platonic Fractals": PDF or HTML or link to(but the pdf version there has lower quality images die to size limits on their server) OpenSource Java Files
|
EEQT or Event-Enhanced-Quantum-TheoryI. EEQT stands for "Event Enhanced Quantum Theory" - the term introduced by Ph. Blanchard and A. Jadczyk to describe the piecewise deterministic algorithm replacing the Schrödinger equation for continuously monitored quantum systems (and we suspect all quantum systems fall under this category). From EEQT FAQ:
II. Most of the essential papers dealing with various aspects of EEQT are available online. III. EEQT allows us to simulate "Nature's Real Working". Of course EEQT is an incomplete theory, yet it tries to simulate the real world events with an underlying quantum substructure. The algorithm of EEQT is non-local, that suggests that Nature itself, in its deeper level, is non-local too. IV. Normally students learning quantum mechanics are being taught that it is impossible to measure position and momentum of a quantum particle. They learn how to derive Heisenberg's uncertainty relations, and they are told that these mathematical relations have such-and-such interpretation. Some are told that the interpretation itself is disputable. In EEQT all the probabilistic interpretation of quantum theory, including Born's interpretation of the wave function, is derived from the dynamics. EEQT allows us to simulate and predict behavior of a quantum system when several, as one normally calls them, incommensurable observables are being measured. The fact is that in such situation the dynamics is chaotic, and no joint probability distribution exists. That explains why ordinary quantum mechanics rightly noticed the problems with defining such a distribution. (For visualization purposes physicists, especially those dealing with quantum chaos, often use Wigner's distribution (which is not positive definite) or Husimi's distribution (which does not reproduce marginal distributions). |
Quantum Jumps |
|
According to EEQT quantum jumps are not directly observable. What we see are the accompanying "events". This part is somewhat tricky, and I will try to explain the trickiness here, in few paragraphs, but without any hope that there will be even one person who will understand what I mean. Well, perhaps mathematicians will do, but are they going to read this page? I doubt. Physicists certainly will think that it is too weird. And they have better things to do than following someone's weird ideas - as every physicist with guts has weird ideas of his/her own! But I would feel guilty if I did not give it a try. So here it is. Physicists do consider quantum jumps. In particular those who deal
with theoretical quantum
optics and/or quantum
computing and information. But these quantum jumps are not being
taken as "real". If not for any other reason, than because
there are infinitely many jump processes that can be associated
with a given Liouville equation, and there is no good reason to
choose one rather than other. Thus discontinuous quantum jumps in
theoretical quantum optics are considered mainly as a convenient
numerical methods for solving the continuous Liouville equation.
It is not so in EEQT. But EEQT splits the world into a quantum and
a classical part, and quantum physicists deny that the classical
part exist. They think all is quantum -
the same way Ptolemeian physicists thought that all is perfectly
round. Can we propose a clever idea that will show that not
all is quantum? Indeed, according to quantum physics the only thing
that exists is the quantum wave function. Now, let us us ask this:
is the wave function itself a classical or a quantum object? That
is, we ask, is location of the wave function in the Hilbert space
governed by classical or by quantum laws? Most quantum physicists
would pretend they do not understand the question. Some will understand,
and will answer: "sure, there is an uncertainty in the state
vector, but that is altogether different story. They will point
me to Braginsky or Vaidman or some other, more recent, paper - but
they will not answer my question: is the quantum wave function a
classical or a quantum object? Is it an object at all? And if it
is an object, then what kind of animal it is, and where it fits?
Philosophers perhaps will point me to Eccles and Popper, but this
is not an answer either. |
|
|
|
To observe itself "It" must split into two "personalities", a quantum one and a classical one. So, here comes the model: consider a pair of wave functions, the function trying to determine its own shape. One element of the pair is considered to be "quantum" - as it determines probabilities and quantum jumps, while the second element of the pair is interpreted as a classical one - its shape is the classical variable.
So, what would be the simplest toy model to play with, that teaches us something about quantum jumps? The quantum system, to be nontrivial, must live in a Hilbert space of at least two complex dimensions. The classical system must have at least two states. Such a toy model was indeed studied in connection to the Quantum Zeno effect., where it was demonstrated that a flip-flop detector strongly coupled (that is "under intensive observation" - watched pot never boils... ) to a two-state quantum system effectively stops the continuous quantum evolution. This model is not interesting though if we want to study pure quantum jumps. Here we need a more complicated model and that is how "tetrahedral model" was developed. It was found that it leads to chaotic dynamics and to fractals of a new type: fractals drawn by a quantum brush on the quantum canvas - a complex projective space. And that is how we come to quantum fractals. |
Quantum Fractals |
|
The canvas, is a surface of the unit sphere In coordinates its points are represented by vectors n = (n1,n2,n3) of unit length, thus (n1)2+(n2)2+(n3)2 = 1. There are five Platonic solids: tetrahedron (N=4), octahedron (N=6), cube (N=8), icosahedron (N=12), dodecahedron (N=20), where N is the number of vertices. They have equal faces, bounded by equilateral polygons. It was Euclid who proved that only five such can exist in a three dimensional world. In his Mysterium Cosmographicum (1595) Johannes Kepler attempted to account for the orbits of the six then known planets by radii of concentric spheres circumscribing or inscribing the solids.
|
|
Last modified on: June 27, 2005.
.
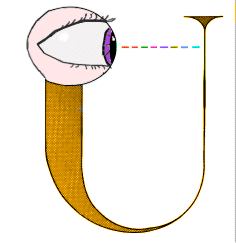 "The
universe viewed as a self-excited circuit. Starting small (thin
U at upper right), it grows (loop of U) to observer participancy
- which in turn imparts 'tangible reality' (cf. the delayed-choice
experiment of Fig. 22.9) to even the earliest days of the universe"
"The
universe viewed as a self-excited circuit. Starting small (thin
U at upper right), it grows (loop of U) to observer participancy
- which in turn imparts 'tangible reality' (cf. the delayed-choice
experiment of Fig. 22.9) to even the earliest days of the universe"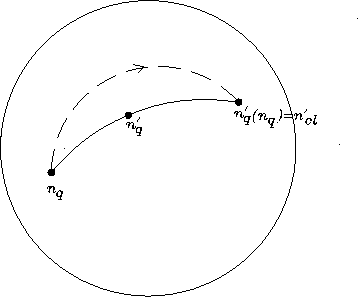 They
dance together and they jump together. More details can be found
in "
They
dance together and they jump together. More details can be found
in " The
details and the bibliography are given in "
The
details and the bibliography are given in "