

Next: 8. Quantum characteristic exponent
Up: 4. Notes
Previous: 6. Continuous part of
There is one important comment that applies here. Even if we
neglect the continuous time evolution due to magnetic field, the
very presence of the detectors causes a non-unitary time evolution
of the pure state of the quantum system. This evolution is also
called, by some physicists (Dicke, Elitzur, Vaidman) ,
"interaction-free". We do not want to enter into this subject
here, except for one remark: for symmetric geometric
configurations that we are considering here, the EEQT algorithm
implies that this, continuous in time, non-unitary evolution can
be neglected as well. In fact, it follows from the EEQT model that
the "interaction-free" or, as we call it, "binamical part" of the
evolution is determined by the generator
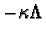 , where
, where
![$\Lambda=\sum P({\bf n}[i],\alpha)^2.$](/quantum_future/papers/qfract/img155.gif) In our case, when our detectors
are symmetrically placed, so that
In our case, when our detectors
are symmetrically placed, so that
![$\sum_{i=1}^N
{\bf n}[i]={\bf0},$](/quantum_future/papers/qfract/img156.gif) the formula (
the formula (![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ) implies
) implies
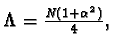 thus the "binamical" part is
just decreasing the norm of the state vector, while leaving its
direction unchanged. Thus it does not affect the geometric pattern
of jumps (it is responsible for the mean frequency of jumps, but
here timing is not important). (For a recent review of EEQT, cf.
[20]
thus the "binamical" part is
just decreasing the norm of the state vector, while leaving its
direction unchanged. Thus it does not affect the geometric pattern
of jumps (it is responsible for the mean frequency of jumps, but
here timing is not important). (For a recent review of EEQT, cf.
[20]


Next: 8. Quantum characteristic exponent
Up: 4. Notes
Previous: 6. Continuous part of
2002-04-11
![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ) implies
) implies
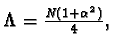 thus the "binamical" part is
just decreasing the norm of the state vector, while leaving its
direction unchanged. Thus it does not affect the geometric pattern
of jumps (it is responsible for the mean frequency of jumps, but
here timing is not important). (For a recent review of EEQT, cf.
[20]
thus the "binamical" part is
just decreasing the norm of the state vector, while leaving its
direction unchanged. Thus it does not affect the geometric pattern
of jumps (it is responsible for the mean frequency of jumps, but
here timing is not important). (For a recent review of EEQT, cf.
[20]