8. Quantum characteristic exponent

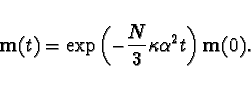
Next: 9. How to measure Up: 4. Notes Previous: 7. Nonunitarity

8. Quantum characteristic exponent

Averaging our nonlinear PDP over individual histories one gets a linear Liouville equation for the density matrix of the total system. Tracing over the classical system is, in our case, easily performed and we then get:

$\begin{displaymath} {\dot \rho}=\kappa (\sum_{i=1}^N P({\bf n}[i],\alpha)\rho P(... ...pha)-\frac{1}{2}\{\sum_{i=1}^N P({\bf n}[i],\alpha)^2 ,\rho\}) \end{displaymath}$

(23)

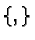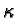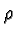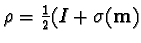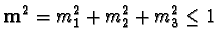where $\{\/ ,\/ \}$ stands for anti-commutator, and $\kappa$ is a coupling constant. For $\rho$ written as $\rho=\frac{1}{2}(I+\sigma({\bf m})$ , ${\bf m}^2=m_1^2+m_2^2+m_3^2\leq 1$ after some calculations we get a very simple time evolution:

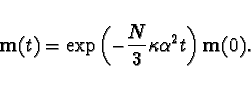$\begin{displaymath} {\bf m}(t)=\exp \left(-\frac{N}{3}\kappa\alpha^2 t\right) {\bf m}(0). \end{displaymath}$

(24)

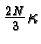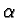The quantum characteristic exponent, as defined in Ref [24], is thus $\frac{2N}{3}\kappa$ - not a very useful quantity in our case. The Hausdorff dimension of the limit set, for the tetrahedral case, has been numerically estimated in Ref. [25] and shown to decrease from 1.44 to 0.49 while $\alpha$ increases from 0.75 to 0.95. We hope that by publishing the generating algorithm we will create interest in confirming these as well as obtaining new results in this field.

Next: 9. How to measure Up: 4. Notes Previous: 7. Nonunitarity

2002-04-11