3. Importance of fuzziness

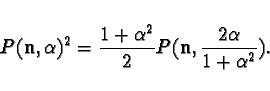
Next: 4. Geometrical meaning of Up: 4. Notes Previous: 2. Fuzzy projections

3. Importance of fuzziness

It is importance to note that in our generalization of the projection postulate, as the result of a jump, not all of the old state is forgotten. The new states depends, to some degree, on the old state. Here EEQT differs in an essential way from the naive von Neumann projection postulate of quantum theory. The parameter 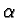$\alpha$ becomes important. If 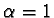$\alpha=1$ - the case where 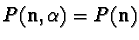$P({\bf n} ,\alpha)=P({\bf n})$ is a projection operator - the new state, after the jump, is always the same, it does not matter what was the state before the jump. There is no memory of the previous state, no "learning" is possible, no "lesson" is taken. This kind of a "projection postulate" was rightly criticized in physical literature as being contradictory to the real world events, contradicting, for instance, the experiments when we take photographs of elementary particles tracks. But when 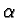$\alpha$ is just close to the value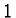

, but smaller than

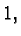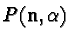the contradiction disappears. This has been demonstrated in the cloud chamber model[9], where particles leave tracks much like in real life, and that happens because the multiplication operator by a Gaussian function does not kill the information about the momentum content of the original wave function. Notice that $P({\bf n},\alpha )$ have the properties similar to those of Gaussian functions, namely

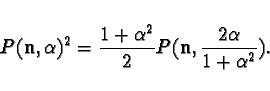$\begin{displaymath} P({\bf n},\alpha)^2=\frac{1+\alpha^2}{2}P({\bf n},\frac{2\alpha}{1+\alpha^2}). \end{displaymath}$

(19)

Next: 4. Geometrical meaning of Up: 4. Notes Previous: 2. Fuzzy projections

2002-04-11