

Next: 1. Pure states as
Up: 4. Notes
Previous: 4. Notes
Pure states of the quantum spin (we are discussing spin 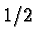 here) are described by unit vectors in our Hilbert space
here) are described by unit vectors in our Hilbert space
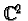 . But, as it is standard in quantum theory, proportional
vectors describe the same state - the overall phase of the vector
has no physical significance. Therefore, in geometrical terms, the
set of all pure states is nothing but the projective complex space
. But, as it is standard in quantum theory, proportional
vectors describe the same state - the overall phase of the vector
has no physical significance. Therefore, in geometrical terms, the
set of all pure states is nothing but the projective complex space
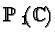 which happens to be the same as the sphere
which happens to be the same as the sphere 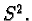 That is why the fractal pattern, in our case, is being drawn on a
spherical canvas. There is, however, another possible
interpretation of the same algorithm. It is well know that there
is an intrinsic relation between Minkowski space and the space of
That is why the fractal pattern, in our case, is being drawn on a
spherical canvas. There is, however, another possible
interpretation of the same algorithm. It is well know that there
is an intrinsic relation between Minkowski space and the space of
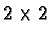 complex Hermitean matrices.
complex Hermitean matrices. ![[*]](/quantum_future/papers/qfract/foot_motif.gif) In
coordinates the map is given by
In
coordinates the map is given by
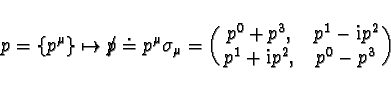 |
(18) |
so that
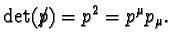 In
particular our projection operators
In
particular our projection operators 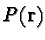 ,
, 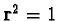 correspond to null directions. In other words our canvas, the
sphere
correspond to null directions. In other words our canvas, the
sphere 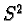 , can be also thought of as the projective light cone
- the space of light directions. Quantum jumps would then
correspond to sudden changes of directions of light or light-like
entities. The formula (
, can be also thought of as the projective light cone
- the space of light directions. Quantum jumps would then
correspond to sudden changes of directions of light or light-like
entities. The formula (![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ) can be easily generalized
for
) can be easily generalized
for 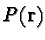 being a generic Hermitean matrix (thus representing
a four-vector
being a generic Hermitean matrix (thus representing
a four-vector  of space- or time-like character as well.
However there is no such generalization for the formula
(
of space- or time-like character as well.
However there is no such generalization for the formula
(![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), so that the probabilities would have to be
assigned equal, and a physical interpretation, even tentative one,
is missing in such a case.
), so that the probabilities would have to be
assigned equal, and a physical interpretation, even tentative one,
is missing in such a case.


Next: 1. Pure states as
Up: 4. Notes
Previous: 4. Notes
2002-04-11
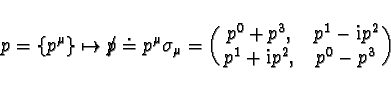
![[*]](/quantum_future/papers/qfract/foot_motif.gif) In
coordinates the map is given by
In
coordinates the map is given by
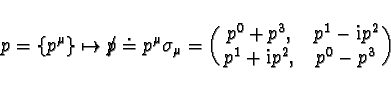
![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ) can be easily generalized
for
) can be easily generalized
for ![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), so that the probabilities would have to be
assigned equal, and a physical interpretation, even tentative one,
is missing in such a case.
), so that the probabilities would have to be
assigned equal, and a physical interpretation, even tentative one,
is missing in such a case.