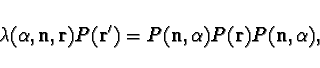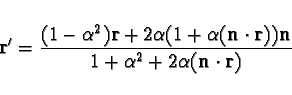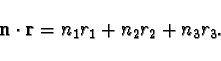

Next: 5. Transition probabilities
Up: 2. The algorithm
Previous: 3. Fuzzy projections
Let us now discuss the algebraic operation that is associated with
each quantum jump. Suppose before the jump the state of the
quantum system is described by a projection operator 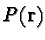 ,
,
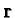 being a unit vector on the sphere. That is, suppose, before
the detector flip, the spin "has" direction
being a unit vector on the sphere. That is, suppose, before
the detector flip, the spin "has" direction 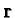 . Now, suppose
the detector
. Now, suppose
the detector
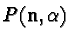 flips, and the spin right after the
flip has some other direction,
flips, and the spin right after the
flip has some other direction,
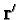 . What is the relation
between
. What is the relation
between 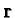 and
and
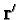 ? It is easy to see that the action
of the operator
? It is easy to see that the action
of the operator
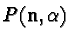 on a quantum state vector is
given, in terms of operators, by the formula:
on a quantum state vector is
given, in terms of operators, by the formula:
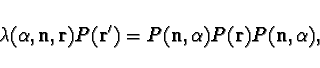 |
(12) |
where
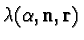 is a positive number. It is a
simple (though somewhat lengthy) matrix computation that leads to
the following result:
is a positive number. It is a
simple (though somewhat lengthy) matrix computation that leads to
the following result:
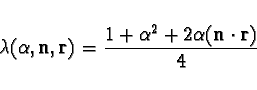 |
(13) |
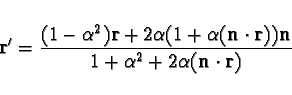 |
(14) |
where
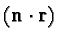 denotes the scalar product
denotes the scalar product
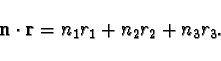 |
(15) |


Next: 5. Transition probabilities
Up: 2. The algorithm
Previous: 3. Fuzzy projections
2002-04-11