

Next: 3. The Five Platonic
Up: 2. The algorithm
Previous: 4. Jumps are implemented
Given the actual state 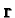 of the quantum system, and the
configuration of the detectors
of the quantum system, and the
configuration of the detectors
![$\{{\bf n}[i], i=1,2,\ldots ,N\}$](/quantum_future/papers/qfract/img85.gif) we
compute probabilities
we
compute probabilities
![$p[i], \sum_{i=1}^N p[i]=1$](/quantum_future/papers/qfract/img86.gif) for the
for the 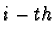 detector to flip. Then we select randomly, with the calculated
probability distribution, the flipping detector, and we implement
the jump by changing
detector to flip. Then we select randomly, with the calculated
probability distribution, the flipping detector, and we implement
the jump by changing 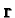 to
to
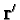 according to the
formula (
according to the
formula (![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), with
), with
![${\bf n}={\bf n}[i]$](/quantum_future/papers/qfract/img88.gif) . The probabilities
. The probabilities
![$p[i]$](/quantum_future/papers/qfract/img89.gif) are computed using the theory of piecewise deterministic
Markov processes applied to the case of quantum measurements - as
developed within EEQT.
are computed using the theory of piecewise deterministic
Markov processes applied to the case of quantum measurements - as
developed within EEQT.![[*]](/quantum_future/papers/qfract/foot_motif.gif) According to EEQT the probabilities
According to EEQT the probabilities ![$p[i]$](/quantum_future/papers/qfract/img89.gif) are given by the formula:
are given by the formula:
![\begin{displaymath}
p[i]=const\cdot\mbox{Tr}\left(P({\bf r})P({\bf n}[i],\alpha)^2P({\bf r})\right)
\end{displaymath}](/quantum_future/papers/qfract/img90.gif) |
(16) |
where 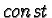 is the normalizing constant. Using cyclic
permutation under the trace, as well as the fact that
is the normalizing constant. Using cyclic
permutation under the trace, as well as the fact that
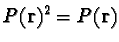 we find, taking trace of both sides of the formula
(
we find, taking trace of both sides of the formula
(![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), that
), that ![$p[i]$](/quantum_future/papers/qfract/img89.gif) are proportional to
are proportional to
![$\lambda(\alpha,{\bf n}[i],{\bf r})$](/quantum_future/papers/qfract/img93.gif) given by (
given by (![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), thus
), thus
![\begin{displaymath}
p[i]=\frac{1+\alpha^2+2\alpha ({\bf n}[i]\cdot {\bf r})}{N(1+\alpha^2)}.
\end{displaymath}](/quantum_future/papers/qfract/img94.gif) |
(17) |
Note that, owing to the fact that
![$\sum_{k=1}^N {\bf n}[k]={\bf0}$](/quantum_future/papers/qfract/img95.gif) we
have
we
have
![$\sum_{i=1}^N p[i]=1$](/quantum_future/papers/qfract/img96.gif) , as it should be.
, as it should be.


Next: 3. The Five Platonic
Up: 2. The algorithm
Previous: 4. Jumps are implemented
2002-04-11
![\begin{displaymath}
p[i]=const\cdot\mbox{Tr}\left(P({\bf r})P({\bf n}[i],\alpha)^2P({\bf r})\right)
\end{displaymath}](/quantum_future/papers/qfract/img90.gif)
![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), with
), with
![[*]](/quantum_future/papers/qfract/foot_motif.gif) According to EEQT the probabilities
According to EEQT the probabilities ![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), that
), that ![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), thus
), thus
![\begin{displaymath}
p[i]=\frac{1+\alpha^2+2\alpha ({\bf n}[i]\cdot {\bf r})}{N(1+\alpha^2)}.
\end{displaymath}](/quantum_future/papers/qfract/img94.gif)