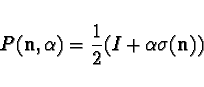 |
(11) |
We restrict the range of the parameter ![]() to the interval
to the interval
![]() because only in this range
because only in this range
![]() is a positive
operator. It is easy to see that this is so. Indeed, a Hermitian
matrix is positive when its eigenvalues are positive, and the
eigenvalues of
is a positive
operator. It is easy to see that this is so. Indeed, a Hermitian
matrix is positive when its eigenvalues are positive, and the
eigenvalues of
![]() are
are
![]() thus
thus
![]() On the other hand negative
On the other hand negative ![]() for
for ![]() is the same as
positive
is the same as
positive ![]() for
for ![]() thus we restrict the range of
thus we restrict the range of
![]() to
to ![]()
It is the operators
![]() that will act on quantum
states to implement "quantum jumps" whenever detectors "flip."
that will act on quantum
states to implement "quantum jumps" whenever detectors "flip."
The overall coefficient in the definition (![[*]](/quantum_future/papers/qfract/cross_ref_motif.gif) ), chosen
to be
), chosen
to be ![]() here, is not important because in applications
each of the operators
here, is not important because in applications
each of the operators
![]() is multiplied by a coupling constant, and, in our case,
when we are not interested in timing of the jumps, the value of
the coupling constant plays no role.
is multiplied by a coupling constant, and, in our case,
when we are not interested in timing of the jumps, the value of
the coupling constant plays no role.