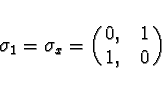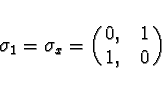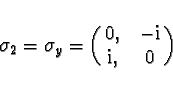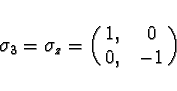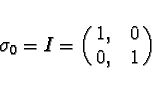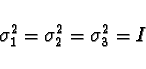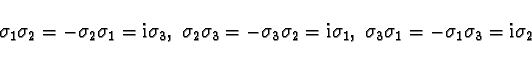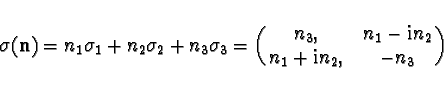

Next: 3. Fuzzy projections
Up: 2. The algorithm
Previous: 1. The Hilbert space
We choose the Pauli matrices
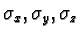 to represent spin directions along
to represent spin directions along
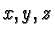 axes respectively.
axes respectively.
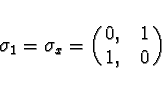 |
(3) |
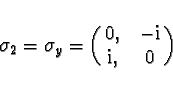 |
(4) |
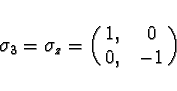 |
(5) |
Together with the identity matrix
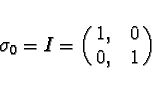 |
(6) |
they span the whole 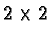 complex matrix algebra. In
computations it is important to make use of the fact that Pauli
matrices (after multiplication by "-i") represent the quaternion
algebra, that is:
complex matrix algebra. In
computations it is important to make use of the fact that Pauli
matrices (after multiplication by "-i") represent the quaternion
algebra, that is:
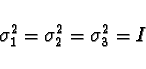 |
(7) |
and
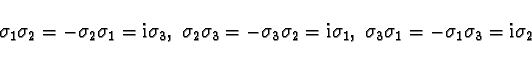 |
(8) |
To each direction 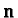 in space there is associated spin matrix
in space there is associated spin matrix
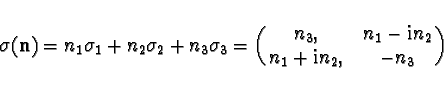 |
(9) |
satisfying automatically
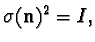 and with eigenvalues
and with eigenvalues
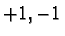 . Vectors
. Vectors
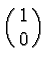 and
and
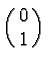 are
eigenvectors of
are
eigenvectors of 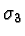 to eigenvalues
to eigenvalues 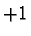 and
and 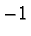 respectively and thus correspond to "North" and "South" spin
orientations respectively. Let
respectively and thus correspond to "North" and "South" spin
orientations respectively. Let 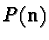 denote the projection
operator that projects onto eigenstate of
denote the projection
operator that projects onto eigenstate of
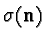 to the
eigenvalue
to the
eigenvalue 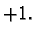 Then
Then 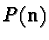 is given by the formula:
is given by the formula:
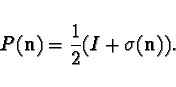 |
(10) |
Indeed, 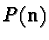 is Hermitian and has eigenvalues
is Hermitian and has eigenvalues
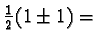
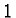 or
or 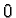 - thus it is the orthogonal
projection, and it projects onto the eigenstate of
- thus it is the orthogonal
projection, and it projects onto the eigenstate of
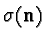 with spin direction
with spin direction 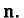


Next: 3. Fuzzy projections
Up: 2. The algorithm
Previous: 1. The Hilbert space
2002-04-11