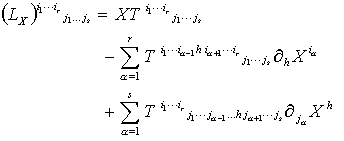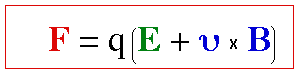Date sent: Tue, 30 Nov 1999 23:55:07 -0800
From: Jack Sarfatti
Send reply to: sarfattiatxwell.com
Organization: Advanced Intelligence Agency
To: RKiehn2352atxaol.com
Copies to: tephippsatxpdnt.com
Subject: Re: Heretical Verities
RKiehn2352atxaol.com wrote:
> HI
> Sommerfeld's ideas are based on thermodynamics.
[Jack]
Yes.
[RK]
>
> **
> If one assumes that the topology of EM involves potentials, then
> in differential form language: F-dA = 0. F has coefficients related to E
> and B, A has coefficients related to the vector and scalar potentials.
> For details see http://www22.pair.com/csdc/pdf/maxwell.pdf
[Jack]
F = dA
implies
dF = 0
since d^2 = 0
But we can have
dF = 0
without having
F = dA
What is the physical meaning of that? That is,
F = dA
is sufficient for
dF = 0
but not necessary.
[RK]
>
> **
> The convective derivative is equivalent to the L:ie derivative with
> respect to an n dimensional direction field V acting on differential
> forms. ***
[Jack]
Is this the same "convective derivative" Phipps uses that Ark objects to?
[RK]
>
> By asking for how the 1-form of A and the 2-form F
> propagate along a direction field
> L(V) A = > Q,
> the Lorentz Force law pops out automatically
> as a derived quantity. IT is NOT added into the theory,
> it falls out from the definition of the Lie derivative.
[Jack]
I think Phipps does this in a more pedestrian way. OK what about the
radiation reaction correction to the Lorentz force law? How can we get
that?
[RK]
>
> The E field is minus grad phi - the partial with respect to time of A
> (not total).
[Jack]
Well this is debatable. What new effects do we get if we use the total
time derivative?
[RK]
>
> The Lie derivative does not depend upon metric or connection, so
> questions of Galilean invariance etc. are moot. The Lie derivative is
> like an operator :partial with respect to t + V grad and acts on tensor
> fields as well as scalar functions. See the pdf file where html
> limitations of mathematic symbols is not a problem.
>
> ***
> Also If you have a DC current flowing in a long wire, and place a
> charged stationary pith ball near the wire, there is no force on the
> pith ball and its motion remains stationary. If however, I give the
> pith ball an initial velocity in a direction, the pith ball experiences
> a force as it does not travel in a straight line. In otherwords there
> is v cross B force but no E force. ** E is not the whole story. Even
> under the assumptions of special relativity it is recognized that if the
> initial magnetic energy density is less than the initial electric energy
> density, then if E dot B = 0, there exists a Lorentz transformation such
> that B= 0 and E is not zero. In such cases E is all that is required.
> However if the magnetic energy density is greater than the electric
> energy density, ( and E dot B =0) then you can find a Lorentz
> transformation such that the E field is Zero, and the B field is not.
> *** The claim that all of electromagnetic theory can be deduced from
> Coulomb's law has a flaw.
[Jack]
Who claims that? I never heard such a claim.
--
"But the real glory of science is that we can find a way of thinking such
that the law is evident. ... For a successful technology, reality must
take precedence over public relations, for Nature cannot be fooled." R. P.
Feynman http://www.well.com/user/sarfatti/
|
From: Arkadiusz Jadczyk
To: Jack Sarfatti ,sarfattiatxwell.com
Subject: Re: Heretical Verities
Date sent: Wed, 1 Dec 1999 06:23:30 -0400
On 30 Nov 99, at 23:55, Jack Sarfatti wrote:
> [RK]
>
> >
> > By asking for how the 1-form of A and the 2-form F
> > propagate along a direction field
> > L(V) A = > Q,
> > the Lorentz Force law pops out automatically
> > as a derived quantity. IT is NOT added into the theory,
> > it falls out from the definition of the Lie derivative.
>
How the Lorenz force pops out? How? It is Lie derivative of what with
respect to what? Lie derivative of a one-form needs derivatives of the
vector field V itself: L_V(A)_i=V^k d_k A_i + A_k d_i V^k while there is
no derivative of V in Lorentz force!
> [Jack]
>
> I think Phipps does this in a more pedestrian way. OK what about the
> radiation reaction correction to the Lorentz force law? How can we get
> that?
I think RK-s statement is incorrect.
ark
|
Date sent: Wed, 01 Dec 1999 22:20:22 -0800
From: Jack Sarfatti
Send reply to: sarfattiatxwell.com
Organization: Advanced Intelligence Agency
To: Arkadiusz Jadczyk
Subject: Re: Heretical Verities
Arkadiusz Jadczyk wrote:
> On 30 Nov 99, at 23:55, Jack Sarfatti wrote:
>
> > [RK]
> >
> > >
> > > By asking for how the 1-form of A and the 2-form F
> > > propagate along a direction field
> > > L(V) A = > Q,
> > > the Lorentz Force law pops out automatically
> > > as a derived quantity. IT is NOT added into the theory,
> > > it falls out from the definition of the Lie derivative.
> >
>
> How the Lorentz force pops out?
[Jack]
Kiehn should answer this. Also Phipps.
[Ark]
> How? It is Lie derivative of what with
> respect to what? Lie derivative of a one-form needs derivatives of the
> vector field V itself: L_V(A)_i=V^k d_k A_i + A_k d_i V^k while there is
> no derivative of V in Lorentz force!
>
> > [Jack]
> >
> > I think Phipps does this in a more pedestrian way. OK what about the
> > radiation reaction correction to the Lorentz force law? How can we get
> > that?
>
> I think RK-s statement is incorrect.
>
> ark
--
"But the real glory of science is that we can find a way of thinking such
that the law is evident. ... For a successful technology, reality must
take precedence over public relations, for Nature cannot be fooled." R. P.
Feynman http://www.well.com/user/sarfatti/
|
From: RKiehn2352atxaol.com
Date sent: Thu, 2 Dec 1999 03:12:54 EST
Subject: Re: Heretical Verities
To: sarfattiatxwell.com, wwwatxcassiopaea.com (Arkadiusz Jadczyk)
Hi
I thought ARK understood the Action of the Lie derivated on forms.
**
For details see
http://www22.pair.com/csdc/pdf/maxwell.pdf
***
in email notation.
on (x,y,z,t)
Let A = Axdx+Aydy+Azdz - phi dt.
Let V=[Vx,Vy,Vz, 1]
Then
L(V)A = i(V)dA + d(i(V)A) = W + dU = Q
For details of Cartan's magic formula see Marsden and Riatu
and my website.
**
Recall that dA generates E and B as components of an 4 x 4 anti-symmetric
matrix based on A. Sommerfeld's 6 vector. ** evaluate virtual work 1-form
W = i(V)dA, get W= (E + VxB) dot dr - (E dot V) dt
= Lorentz force times differential distance - (power) dt
****
For currents of the type J = rho V
Evaluate L(J) A = W +dU
with virtual work evaluated as
W = i(J)dA = (rho E + JxB) dot dr - (E dot J) dt
***
QED
regards
RMK
|
From: RKiehn2352atxaol.com
Date sent: Thu, 2 Dec 1999 08:17:01 EST
Subject: Lorentz force
To: wwwatxcassiopaea.com (Arkadiusz Jadczyk)
Copies to: sarfattiatxwell.com
HI
I think you mis-read, or put your own interpretation on what I stated. See
the pdf attachment. Regards RMK
|
From: Arkadiusz Jadczyk
To: sarfattiatxwell.com,RKiehn2352atxaol.com
Subject: Re: Heretical Verities
Date sent: Thu, 2 Dec 1999 06:45:07 -0400
On 2 Dec 99, at 3:12, RKiehn2352atxaol.com wrote:
> Hi
> I thought ARK understood the Action of the Lie derivated on forms.
> **
He does
> For details see
> http://www22.pair.com/csdc/pdf/maxwell.pdf
> ***
He has better sources.
> in email notation.
> on (x,y,z,t)
> Let A = Axdx+Aydy+Azdz - phi dt.
> Let V=[Vx,Vy,Vz, 1]
Why the fourth component of V must be 1? But
it is not important for our problem.
> Then
> L(V)A = i(V)dA + d(i(V)A) = W + dU = Q
In coordinates this is the same as my formula, because
i(V)dA has two terms, d(i(V)A) has two terms, altogether
four terms, but two of them cancel!
Do you want to see it?
Here it is:
Compute the first term:
1) (dA)_ij = d_i A_j - d_j A_i
Therefore
2) [ i(V)dA ]_j = V^i (dA)_ij = V^i d_i A_j - V^i d_j A_i
Compute the second term (using Leibniz rule)
3) d(i(V)A)_j = d_j [ V^i A_i ] = d_j (V^i) A_j + V^i d_jA_i
Now, when you add 2) and 3) , you see that second terms
cancel and we get simple
(L(V)A)_j = V^i d_i A_j + d_j (V^i) A_j
Which was my formula. Thus, as you see, Ark knows about
Lie derivative. Ark even wrote a paper (with Daniel Kastler)
"Graded Lie-Cartan pairs", and "Graded Lie-Cartan Pairs II"
Annals of Physics (NY) 179, No 2 (1987), 169-200
> For details of Cartan's magic formula see Marsden and Riatu
> and my website.
> **
It is not necessary
> Recall that dA generates E and B as components of an 4 x 4
> anti-symmetric matrix based on A. Sommerfeld's 6 vector. ** evaluate
> virtual work 1-form W = i(V)dA, get W= (E + VxB) dot dr - (E dot V) dt
> = Lorentz force times differential distance - (power) dt
> ****
THis does not matter. Lie derivative of A with respect V
does contain partial derivatives of V while Lorentz term
does not have them.
> For currents of the type J = rho V
> Evaluate L(J) A = W +dU
> with virtual work evaluated as
> W = i(J)dA = (rho E + JxB) dot dr - (E dot J) dt
THis does not matter. Lie derivative of A with respect V
does contain partial derivatives of V while Lorentz term
does not have them!!!!
AGREE??? Or should I be even more clear?
ark
|
From: Arkadiusz Jadczyk
To: RKiehn2352atxaol.com
Subject: Re: Lorentz force
Copies to: sarfattiatxwell.com
Date sent: Thu, 2 Dec 1999 10:15:43 -0400
> HI
> I think you mis-read, or put your own interpretation on what I stated.
> See the pdf attachment. Regards RMK
No,
I did not mis-read. You now say that "non-exact" component of Lie
derivative gives Lorentz force. Well, what about "exact" component?
Is it not in violation of the Lorenz force? It is.
You see, I can make a component of EVERYTHING to give Lorentz force.
Say, I have anynmagic formula A, and denote Lorentz force by L
Then I will write
A = B+L
where B=A-L
Magic, I have now a component of A giving exactly the Lorentz force!!!
Magic or slight of hand?
Your statement
> > > the Lorentz Force law pops out automatically
> > > as a derived quantity. IT is NOT added into the theory,
> > > it falls out from the definition of the Lie derivative.
hides the fact that there is also a second term which
involves derivatives of V, and which contradics
Lorentz force. Your statement that Lorentz
force is not added to the theory is thus incorrect.
Best,
ark
|
From: RKiehn2352atxaol.com
Date sent: Thu, 2 Dec 1999 14:28:58 EST
Subject: Re: Lorentz force
To: wwwatxcassiopaea.com, sarfattiatxwell.com
IF I remember my training the Lorentz force is defined as
E + V x B on a unit charge moving with V.
DO YOU DISAGREE OR AGREE.
**
It appears to me that W = i(V)dA generates that formalism.
E + V x B
DO YOU AGREE OR DISAGREE
***
There are no derivatives of V in the expression for W
DO YOU AGREE OR DISAGREE
***
The definition of W also indicates that
F(Lorentz) dot V = E.V, for any V,
the power theorem that I learned long ago
as being useful in applied electromagnetism.
**
I believe you have something to reconsider.
Perhaps your "sources" need reinvestigation.
**
The same method applied to the
1-form
A = v dot dr - (v^2+phi )dt
will generate the Euler fluid equations.
**
Searching for solutions where
d(i(V)dA) <> 0
will generate Navier Stokes equations.
**
The equations of motion come form W = i(V)dA
in the calculus of variations and in forms language.
**
Cartan demonstrated the any form A
such that i(V)dA = d(theta)
had equations of motion such that the V were of the
Hamiltonian format. (an iff theorem)
His proof (see Lessons on Integral Invariants) was deduced
by searching for evolutionary fields V
such the the closed integral of A was an invariant.
HEnce:
Lie derivative of closed integral of A = 0 is necessary and sufficient. **
In that case the perfect differentials in the definition of the Lie
derivative do not contribute, for the closed integral of a perfect
differential is zero. NOte also that dA is an evolutionary invariant of a
HAmiltonian system as L(V)dA = dd(theta) = 0. A restatement of the
Helmhoiltz theorem (and related to gauge invariance) which leads to the
invariance of the even dimensional Poincare integrals. *** Another fact of
cohomology. HOW CAN I BE MORE CLEAR. RMK
|
From: Arkadiusz Jadczyk
To: RKiehn2352atxaol.com
Subject: Re: Lorentz force
Copies to: Jack Sarfatti
Date sent: Thu, 2 Dec 1999 15:53:33 -0400
On 2 Dec 99, at 14:28, RKiehn2352atxaol.com wrote:
> IF I remember my training the Lorentz force is defined as
> E + V x B on a unit charge moving with V.
> DO YOU DISAGREE OR AGREE.
agree
> It appears to me that W = i(V)dA generates that formalism.
> E + V x B
> DO YOU AGREE OR DISAGREE
Yes, this is how Lorentz force is always represented
in a relativistic form - assumingthe fourh component of
four-velocity being = 1.
> There are no derivatives of V in the expression for W
> DO YOU AGREE OR DISAGREE
agree
> ***
> The definition of W also indicates that
> F(Lorentz) dot V = E.V, for any V,
> the power theorem that I learned long ago
> as being useful in applied electromagnetism.
> **
I do not know what is your notation. It becomes
now confusing.
1) What is F(Lorentz)?
Is F(Lorentz) = E + V x B
as above?
What is dot V? How you calculate dot V?
Is it the same V as in the Lorentz force?
Is time derivative computed along trajectory
of the charged particle? If so, then I disagree.
Or is dot a scalar product symbol? If it is
a scalr product, yes
F(Lorentz).V = (E + V x B).V = E.V because VxB is perpendicular to V
**********************************************
> I believe you have something to reconsider.
> Perhaps your "sources" need reinvestigation.
Which sources?
> **
> The same method applied to the
> 1-form
> A = v dot dr - (v^2+phi )dt
> will generate the Euler fluid equations.
> **
I do not know what you are talking about now.
What "aplies" THE SAME WAY?
> Searching for solutions where
> d(i(V)dA) <> 0
> will generate Navier Stokes equations.
> **
What is the relation of this to the first part?
There is no relation. You are now consider
a different problem, and you do not even
try to explain what is this new problem.
> The equations of motion come form W = i(V)dA
> in the calculus of variations and in forms language.
> **
You have to explain what you mean. I have no idea.
> Cartan demonstrated the any form A
> such that i(V)dA = d(theta)
> had equations of motion such that the V were of the
> Hamiltonian format. (an iff theorem)
What equation of motions? In which framework?
In which context?
> His proof (see Lessons on Integral Invariants) was deduced
> by searching for evolutionary fields V
> such the the closed integral of A was an invariant.
Proof of what? Can you state the exact theorem you are now
talking about? And how it relates to Lorentz force?
> HEnce:
> Lie derivative of closed integral of A = 0 is necessary and sufficient.
> **
What is the stament? While the first part, where you were asking me,
whether I agree or not, was clear (and I agreed, but it was irrelevant),
now you are using vague terms.
> In that case the perfect differentials in the definition of the Lie
> derivative do not contribute, for the closed integral of a perfect
> differential is zero.
There are no derivatives of V in the Lorentz foce. Therefore
Lie derivative cannot help you to get it.
> NOte also that dA is an evolutionary invariant of a HAmiltonian system
> as L(V)dA = dd(theta) = 0.
What are you talking about and how it relates to Lorentz force?
There are no derivatives of V in the Lorentz foce. Therefore
Lie derivative cannot help you to get it.
> A restatement of the Helmhoiltz theorem (and related to gauge
> invariance) which leads to the invariance of the even dimensional
> Poincare integrals. *** Another fact of cohomology. HOW CAN I BE MORE
> CLEAR.
By keeping to the standard of clarity. You were doing well
before the line ************************************
But you gave up after ************************** and
what was after is either irrelevant or incomprehensible.
There is no derivative of V in the formula for the
Lorentz force. There are derivatives of V in the formula
for Lie derivative of vector potential. Therefore othey are two
essentially different things. You can't put derivatives ov V
under the rug. They will call from there:
"WE ARE HERE!!!!!!!!!!" They will go after you, they
will haunt you, and calling names Cartan and Euler (and
even Hamilton) will not help. They will not disappear!
Best,
ark
|
From: RKiehn2352atxaol.com
Date sent: Fri, 3 Dec 1999 13:36:59 EST
Subject: Lorentz Force
To: wwwatxcassiopaea.com (Arkadiusz Jadczyk)
Copies to: sarfattiatxwell.com
Hi
see pdf attachmentment
Also try not to put your own spin on what I say.
Regards
RMK
|
From: Arkadiusz Jadczyk
To: RKiehn2352atxaol.com
Subject: Re: Lorentz Force
Copies to: sarfattiatxwell.com
Date sent: Fri, 3 Dec 1999 16:46:58 -0400
So you say:
"What is your hang up here? My claim is that the Lorentz force
comes from the non-exact component of the Lie derivative.
That component does NOT contain Lie derivatives of V"
That is partially true. Why only partially, I will explain in a while. And
what is my hung up? It is that that Lie derivative HAS derivatives of V
and therefore is IRRELEVANT for the discussion of the Lorentz force. It is
simply WRONG to associate Lorentz force with Lie derivative. They are
simply TWO DIFFERENT ANIMALS.
And second, let me explain to you, why even what you said above is only
partially correct. Lie derivative is a general geometrical tool. You can
apply it to any tensor field. Covariant, contravariant, even to tensor
densities of any kind. And it is defined this way in any good book. Then
you can apply this definition to a one form. In particular. So you
calculate FROM THE DEFINITION. And what you get? You get two terms:
L(V)A_i = V^j d_j A_i + d_i V^j A_J
No one of these two terms has anything to do with the Lorentz force.
I repeat: NO OF THESE TWO.
But THEN, and ONLY THEN, there comes a THEOREM.
Why not substract and add a term - to see if we can write
the above in another form that we may recognize as something?
So, you start playing the game of substractin and adding the same term:
L(V)A_i = V^j d_j A_i + d_i V^j A_J + 0
True? Sure
0 = V^i d_i A_j - V^i d_i A_j
True? Sure!
Therefore:
L(V)A_i = V^j d_j A_i + d_i V^j A_J + 0 = V^j d_j A_i + d_i V^i
A_J + V^j d_i A_j - V^j d_i A_j
And now, why not rearrange? Let us write 1 and 4 termes first and 2 and 3
terms after:
L(V)A_i = (V^j d_j A_i - V^j d_i A_j) + (d_i V^j A_J + V^j d_i A_j)
Oh, now we, see: the first bracket can be written as i(V) dA
And the second bracket can be written as d(i(V)A)!
Amazing!
But, you see, we arrived at this THEOREM doing something with
the original formula. In fact, we were playing the game of adding
and substracting, arriving from simple, original two terms to FOUR terms!
Will you be surprised if using the same method I will arrive even at more
fancy formulas, with eight terms? Or with 1024 terms? One of which will be
Dirac operator? Will you say then that Dirac operator "pops out"? Anything
can "po out" this way.
NO, no, no. Lie derivative, when you use its DEFINITION, and if you
are not plaing tricks of add and subtract, gives :
L(V)A_i = V^j d_j A_i + d_i V^j A_J
and there is NO i(V)dA here.
Second: Lie derivative contains derivatives of V and therefore
relating it to Lorentz force IS MISLEADING. It has NOTHING
to do with the Lorentz force. NOTHING.
Am I hang up? Yes, certainly. I value clarity.
And, for your info. Lie derivative is introduced in Bishop
and Goldberg "Tensor Analysis on Manifolds" on p. 129,
Ch. 3. An explicit formula (3.6.1) is derived from the definition,
and it is the formula that I am using.
Then, ONLY THEN, in Ch 4, p 172, fourty
pages further on, we have a THEOREM,
which tells us that for differential forms it can ALSO
be represented using i and d operators. The proof takes
almost a page, but it reduces effectively to what I have done above:
to adding and substracting a term.
Therefore, what follows from all of the above is this: Lorentz
force pops out naturally from the Lorentz force. But, if we
want to play tricks adding and subtracting terms, then Lorentz
force can pop out even from Grothendick topological invariant of 127
class! Why not??? It can "pop out" from anywhere.
Associating Lorentz force with Lie derivative of vector potential
is, therefore. MISLEADING those people who are not fluent
in differential geometry. Those who know the terms in an intuitive
way, but are not prefessional geometers. I am interveening here
to defend those poor friends of ours. They are your friends to.
They deserve clarity and truth.
Best wishes,
ark
|
From: Arkadiusz Jadczyk
To: Tom Phipps
Subject: Re: Heretical Verities
Copies to: RKiehn2352atxaol.com,Jack Sarfatti
Date sent: Fri, 3 Dec 1999 19:42:48 -0400
On 3 Dec 99, at 16:00, Tom Phipps wrote:
> Just so -- I use ordinary vector analysis. If I paid more attention to
> polar vs. axial vectors it might make people like Kiehn and Post
> happier. But let me set that aside and remark that the total time
> derivative of vector potential, if used in the Hertzian (first-order
> invariant) force law, F = q E(Hz) = q (-grad(phi) - dA/dt), does indeed
> cause the Lorentz force law to "pop out," but in addition there pops out
> a gradient term, minus grad(A dot v), where v = v(t) is velocity of the
> test charge q.
First: To compute the term grad(A dot v) we need ALL derivatives of v, not
only along the trajectory! Therefore can not be interpreted as velocity of
the charge. If v is velocity of the charge, then v=dx/dt and there is no
way to compute its partial derivatives!
Second, extra term to Lorentz force is very easy to test experimentally,
because this extra term would change curvature of particle tracks in every
cyclotron. It would cause loses of milions of dollars if it existed and
was not known to engineers that were building cyclotrons in Hamburg and in
Geneve!
ark
To
> show this just requires one of the standard vector identities. Thus
> there is a less sophisticated route to the Kiehn result, but with a
> twist -- that an extra gradient term appears, which integrates to zero
> around any closed circuit and thus is very hard to verify in the lab.
|
From: RKiehn2352atxaol.com
Date sent: Sat, 4 Dec 1999 05:48:38 EST
Subject: Re: Lorentz Force
To: wwwatxcassiopaea.com
Copies to: sarfattiatxwell.com
Hi
In my opinion you still have a hangup, but that is your right.
*
Adding and subtracting terms to organize mathematical structures has its
place. For example, in linear algebra, given an arbitrary matrix, the
addition and subtraction of the matrix transpose, to form the symmetric
and anti-symmetric parts is a very useful technique. In cohomology the
addition and subtraction of various constructions to lead to objects whose
difference is characterized by a perfect differential is the cornerstone
of the theory. Note that the Cartan formulation of the "Lie derivative"
acting on differential forms is precisely a cohomological method. I
believe it is you who do a disservice by claiming that these methods are
not useful. *** I state again, the LORENTZ force IS NOT THE LIE
DERIVATIVE acting on CONTRAVARIANT OBJECTS. Neither is the Lorentz force
equal to THE LIE DERIVATIVE acting on covariants (differential forms) **
The Lie derivative with respect to V acting on a covariant exterior
1-form A has two parts. The first part, W = i(V)dA which is not
necessarily closed, and a second part which is exact d(U) = d(i(V)A).
The LORENTZ FORCE IS REPRESENTED BY THE COVARIANT COMPONENTS OF THE FIRST
PART OF THE CARTAN FORMULA. W=i(V)dA IT DOES NOT INCLUDE THE EXACT PART
dU OF THE CARTAN FORMULA
***
I suggest that you should read
Marsden and Riatu "Introduction to mechanics and symmetry" Springer-Verlag
1994 page 122 . on Cartan's MAgic formula, and P. Libermann "Symplectic
Geometry and Analytical Mechanics" Riedel p.368 and p.376. on why
contravariant formalisms are not as good as covariant formalisms ( the
second order jets on contravariants do not form a vector space, while the
second order jets on the covariants do form a vector space.)
Differential Geometry in terms of differential forms has its advantages,
as told to me by Professor Chern, and utilized by him to generate many
interesting theorems.
Regards
RMK
|
From: RKiehn2352atxaol.com
Date sent: Sat, 4 Dec 1999 05:54:29 EST
Subject: Lorentz force again
To: tephippsatxpdnt.com (Tom Phipps)
Copies to: sarfattiatxwell.com, wwwatxcassiopaea.com (Arkadiusz Jadczyk)
Subj: Re: Heretical Verities
Date: 12/4/99 1:44:15 AM Central Standard Time
From: sarfattiatxwell.com (Jack Sarfatti)
Tom Phipps wrote:
.....
> Just so -- I use ordinary vector analysis. If I paid more attention to
> polar vs. axial vectors it might make people like Kiehn and Post
> happier. But let me set that aside and remark that the total time
> derivative of vector potential, if used in the Hertzian (first-order
> invariant) force law, F = q E(Hz) = q (-grad(phi) - dA/dt), does indeed
> cause the Lorentz force law to "pop out," but in addition there pops out
> a gradient term, minus grad(A dot v), where v = v(t) is velocity of the
> test charge q.
[RMK SAYS]
I do not have a copy in France, and so have not read your book.
My apologies.
However.
Using Cartan's Magic Formula for the action of the Lie derivative on forms
gives the basic result: Propagation of a 1-form of Action down a tube of
trajectories generated by a vector field (in 4D) yields the following two
term decomposition:
"DAction/ds" = (Lorentz force dot dr) + grad(A.v -phi) - (E.V -partial(
A.v -phi) /dt) dt
= {(Lorentz force dot dr) -(E.v)dt} + {a perfect
differential that involves v}
Without your book I am not sure that this is precisely what you say, but
the Cartan formalism gives a result that seems to be similar to your words
-- (however you managed to derive the result). The major difference - it
would appear - is that the function is (A dot v - phi), not just Adotv
If I interpret Ark properly, it seems that he objects to the Cartan
decomposition formula, for it does not seem to agree with the concept of
the Lie derivative as applied to contravariant vectors. However Cartan's
formula is defined on differential forms, whose component functions are
covariant, not contravariant.
**
There is a fundamental (important and little recognized) fact that
contravariant fields do not behave the same as covariant fields relative
to maps (transformations or processes) that are continuous, but do not
preserve topology. The antisymmetric covariant fields, which are the
working objects of differential forms, are well behaved wrt to such
transformations, while the contravariant fields are not. see
http://www22.pair.com/csdc/pdf/retrodic.pdf *** I refer everyone to
Marsden and Riatu "Introduction to mechanics and symmetry" Springer-Verlag
1994 page 122 . Marsden (who I consider to be one one of the best) is
the one that gave the name "Cartan's Magic Formula" to the formalism of
the Lie derivative acting on differential forms. I have read (if my
memory does not fail me), but do not have the reference here in France,
that Slebodzinsky is the one who coined the word Lie derivative, after
Cartan's work on exterior differential forms, and not in direct reference
to Sophus Lie.
(Recall Cartan's thesis was in large part a rework and extension of Lie
theory, but written in terms of covariants, and not contravariants.) **
> show this just requires one of the standard vector identities.
> Thus there is a less sophisticated route to the Kiehn result, but with a
> twist -- that an extra gradient term appears, which integrates to zero
> around any closed circuit and thus is very hard to verify in the lab.
> Let's say it has never been verified, but I think also never refuted.
> The justification for playing such games is that (d/dt)' = d/dt, i.e.,
> the total time derivative operator is Galilean invariant, whereas the
> particle time derivative operator is not. I claim that one wants
> first-order invariance, in fact invariance at every order of
> approximation ... otherwise there would exist an order of approximation
> at which not all observers would agree on what they were observing.
> Certainly first order takes priority, since in practice that may be the
> only order observable at all. It is a peculiarity of Einstein and his
> followers that they skip over the first order (and its legitimate
> demands for invariance) and go at once to O[(v/c)^2] ... where they
> settle for covariance. Since that is not the way physicists think
> (about orders of approximation), it is apparent that in this century
> physics has fallen into the hands of nonphysicists.
>
> Best, Tom.
[RMK SAYS]
One of the remarkable features of the Lie derivative acting on
differential forms is that it is a concept that does not depend upon
metric nor upon connection. It has the "appearances" of a hydrodynamic
derivative propagating things down flow lines. But questions of Galilean
invariance are not germain, for the concept is valid on every reference
system for which first partial derivatives can be defined. ** As yet
another exhibition of the distinction between covariants and
contravariants, note that the second jet bundle on contravariants does not
form a vector space, while the second and higher jet bundles on covariants
are vector spaces. (The jet bundles are saying something about the degree
of contact of one curve to another.) This result was not something that
came to me intuitively. (I learned this from the book by Paulette
Libermann on Symplectic geometry.) The first jet bundle on either
contravariant or contravariant forms a vector space, but not the second
jet bundle. It is another result that emphasizes the topological
differences between contravariants and covariants (which are merely
alias-alibi objects relative to diffeomorphisms which preserve topology)
*** In physics note that most "wave properties" are covariant and most
"particle" properties are contravariant. However particles are equivalent
to waves only under limited circumstances. (Copenhagen enthusiasts seem
to ignore this fact.) ** For Dr. Phipps, the point of this discourse is (
IMO ) that linearity (first jet) is not the whole show, and at the
non-linear level care should be taken to insure that contravariants should
not be mixed with covariants, especially in non-linear systems where
attention to the second and higher order jets needs to be taken into
account. Bottom line: You are safe if your formulation can be made in
terms of differential forms. (A useful theory, which I would hope, as the
years go by, that more and more folks - both scientists and engineers --
would learn).
***
Regards
RMK
|
From: Arkadiusz Jadczyk
To: RKiehn2352atxaol.com
Subject: Re: Lorentz Force
Copies to: Jack Sarfatti ,Tom Phipps
Date sent: Sat, 4 Dec 1999 09:28:40 -0400
On 4 Dec 99, at 5:48, RKiehn2352atxaol.com wrote:
> Hi
> In my opinion you still have a hangup, but that is your right.
> *
> Adding and subtracting terms to organize mathematical structures has its
> place.
I never said it does not. Surely it does.
> For example, in linear algebra, given an arbitrary matrix, the
> addition and subtraction of the matrix transpose, to form the symmetric
> and anti-symmetric parts is a very useful technique.
Sure! But to claim that antisymmetric matrix "pops out"
of an arbitrary matrix would be unfair unfair!!!!
> In cohomology the
> addition and subtraction of various constructions to lead to objects
> whose difference is characterized by a perfect differential is the
> cornerstone of the theory.
Sure! But to claim that antisymmetric matrix "pops out"
of an arbitrary matrix would be unfair unfair!!!!
> Note that the Cartan formulation of the "Lie derivative"
> acting on differential forms is precisely a cohomological method.
Lie derivative has been invented before Cartan, and it is a general
mathematical concept. IT applies to ANY geometrical object on
a manifold!!! Then you can restrict it to differential
forms and see if it can be expressed in terms of operation on
forms, that is i and d. And sure it can!. But it takes a little
while. Cartan had to COMPUTE, to prove a theorem, in
order to find expression of Liee derivative in terms of i and d.
> believe it is you who do a disservice by claiming that these methods are
> not useful. ***
I am not claiming that these (or other) methods are not
useful. I am claiming that what you say is IRRELEVANT
to the problem at hand, which is DERIVING EXPRESSION FOR THE
LORENTZ FORCE!
> I state again, the LORENTZ force IS NOT THE LIE
> DERIVATIVE acting on CONTRAVARIANT OBJECTS. Neither is the Lorentz force
> equal to THE LIE DERIVATIVE acting on covariants (differential forms) **
> The Lie derivative with respect to V acting on a covariant exterior
> 1-form A has two parts. The first part, W = i(V)dA which is not
> necessarily closed, and a second part which is exact d(U) = d(i(V)A).
If you wish, you can make it to have not only two parts, but also
FOUR PARTS! By adding and substracting terms.
> The LORENTZ FORCE IS REPRESENTED BY THE COVARIANT COMPONENTS OF THE
> FIRST PART OF THE CARTAN FORMULA. W=i(V)dA IT DOES NOT INCLUDE THE
> EXACT PART dU OF THE CARTAN FORMULA
And the second part is WRONG if you attempt to associate it with the
Lorentz force. Therefore to associate Lie derivative with Lorentz force is
MISLEADING! And this is what I say. To my student I would even say: IT IS
WRONG. YOU HAVE TO DO YOUR HOMEWORK BETTER. YOU MUST ANALYZE FIRST! But to
you, to Jack, to Tom, I am just saying this: IT IS MISLEAFING. Neither
Jack nor Tom are specialist in differential geometry. They could even
believe you that mixing Cartan and cohomology gives Lorentz force. But
this is NOT TRUE! It is MISLEADING! > > *** > > I suggest that you should
read > Marsden and Riatu "Introduction to mechanics and symmetry"
Springer-Verlag > 1994 page 122 . on Cartan's MAgic formula, and P.
Libermann "Symplectic > Geometry and Analytical Mechanics" Riedel p.368
and p.376. on why > contravariant formalisms are not as good as covariant
formalisms ( the > second order jets on contravariants do not form a
vector space, while the > second order jets on the covariants do form a
vector space.)
So what? You can not ANY differential geometry without contravariant
tensors. Remember, first you have tangent space (which are
contravariant vectors) and only THEN you define differential forms
as DUAL space. Some geometrical objects are vectors, some
are forms. Some are mixed objects. Don't you know all that?
>
> Differential Geometry in terms of differential forms has its advantages,
NONSENSE - as Jack would say!
> as told to me by Professor Chern, and utilized by him to generate many
> interesting theorems.
Sure, you can prove many interesting thorems about ANY object.
You do not need to talk to Chern to realize this simple fact.
>
> Regards
> RMK
You are welcome.
ark
|
From: Arkadiusz Jadczyk
To: RKiehn2352atxaol.com
Subject: Re: Lorentz force again
Copies to: sarfattiatxwell.com, wwwatxcassiopaea.com (Arkadiusz Jadczyk)
Date sent: Sat, 4 Dec 1999 09:40:37 -0400
On 4 Dec 99, at 5:54, RKiehn2352atxaol.com wrote:
> Without your book I am not sure that this is precisely what you say, but
> the Cartan formalism gives a result that seems to be similar to your
> words
> -- (however you managed to derive the result). The major difference -
> it
> would appear - is that the function is (A dot v - phi), not just Adotv
>
> If I interpret Ark properly, it seems that he objects to the Cartan
> decomposition formula,
No, Ark simply pointed you out to a PROOF of this formula in
the book of Bishop and Goldberg. Ark also showed you how one
proves this formula for 1-forms: by adding and subtracting terms.
> for it does not seem to agree with the concept of
> the Lie derivative as applied to contravariant vectors.
Incorrect. WRONG! FALSE. Lie derivative applies and is
defined FOR ANY GEOMETRICAL OBJECT
(say to any tensor density of whatever weight, whatever
contravariant and covariant ranks). Then, for differential
forms, which are covariant antisymmetric tensors, you
can ALSO represent Lie derivative in a different form, and
this different form is obtained by adding and subtracting
appropriate terms.
> However Cartan's
> formula is defined on differential forms, whose component functions are
> covariant, not contravariant.
See above. Cartan PROVED this formula starting with the
DEFINITION of Lie derivative. He did not invent it!
>
> **
> There is a fundamental (important and little recognized) fact that
> contravariant fields do not behave the same as covariant fields relative
> to maps (transformations or processes) that are continuous,
Sure. But it is not little recognized. It is the FIRST thing that
you learn in differential geometry.
> but do not
> preserve topology.
> The antisymmetric covariant fields, which are the
> working objects of differential forms, are well behaved wrt to such
> transformations, while the contravariant fields are not. see
> http://www22.pair.com/csdc/pdf/retrodic.pdf *** I refer everyone to
> Marsden and Riatu "Introduction to mechanics and symmetry"
> Springer-Verlag 1994 page 122 . Marsden (who I consider to be one one
> of the best) is the one that gave the name "Cartan's Magic Formula" to
> the formalism of the Lie derivative acting on differential forms.
It has nothing to do with Lorentz force and with problem at hand, which is
whether Lie derivative is relevant for this or not.
> I have read (if my
> memory does not fail me), but do not have the reference here in France,
> that Slebodzinsky is the one who coined the word Lie derivative, after
> Cartan's work on exterior differential forms, and not in direct
> reference to Sophus Lie.
> (Recall Cartan's thesis was in large part a rework and extension of Lie
> theory, but written in terms of covariants, and not contravariants.) **
It has nothing to do with Lorentz force and with problem at hand, which is
whether Lie derivative is relevant for this or not.
> > show this just requires one of the standard vector identities.
> > Thus there is a less sophisticated route to the Kiehn result, but with
> > a twist -- that an extra gradient term appears, which integrates to
> > zero around any closed circuit and thus is very hard to verify in the
> > lab.
It has nothing to do with Lorentz force and with problem at hand, which is
whether Lie derivative is relevant for this or not.
> > Let's say it has never been verified, but I think also never refuted.
> > The justification for playing such games is that (d/dt)' = d/dt, i.e.,
> > the total time derivative operator is Galilean invariant, whereas the
> > particle time derivative operator is not.
It has nothing to do with Lorentz force and with problem at hand, which is
whether Lie derivative is relevant for this or not.
I claim that one wants
> > first-order invariance, in fact invariance at every order of
> > approximation ... otherwise there would exist an order of
> > approximation at which not all observers would agree on what they were
> > observing. Certainly first order takes priority, since in practice
> > that may be the only order observable at all.
It has nothing to do with Lorentz force and with problem at hand, which is
whether Lie derivative is relevant for this or not.
It is a peculiarity of Einstein and his
> > followers that they skip over the first order (and its legitimate
> > demands for invariance) and go at once to O[(v/c)^2] ... where they
> > settle for covariance.
It has nothing to do with Lorentz force and with problem at hand, which is
whether Lie derivative is relevant for this or not.
Since that is not the way physicists think
> > (about orders of approximation), it is apparent that in this century
> > physics has fallen into the hands of nonphysicists.
It has nothing to do with Lorentz force and with problem at hand, which is
whether Lie derivative is relevant for this or not.
ark
|
From: RKiehn2352atxaol.com
Date sent: Sat, 4 Dec 1999 16:25:06 EST
Subject: Re: Lorentz Force
To: wwwatxcassiopaea.com
Copies to: sarfattiatxwell.com, tephippsatxpdnt.com (Tom Phipps)
Hi
I DO NOT say that the LORENTZ force has anything to do with dU
I have said that the Lorentz Force format has to do with the other part
of
the Cartan
formula describing the Lie derivative acting on differential forms.
IT IS GENERATED by the term W-=i(V)dA NOT dU
IT has nothing to do with dU!
Why do you keep trying to say that the LORENTZ force involves dU,
I DO NOT SAY THAT --- THAT IS YOUR SPIN, not mine.
The crucial issue is that the format E + V x B is indeed deducible from
the
expression i(V)dA
-- which ( I presume) you now concede is indeed part of the Lie derivative
construction called Cartan's magic formula. L(V)A = i(V)dA + d(i(V)A)
I suggest again that you read Marsden.
**************
**************
DO YOU AGREE or DISAGREE that the format
E + VxB comes from i(V)dA.
*************
*************
If you say yes then we are done, for my point is made.
if you say no, then you are incorrect.
*************
*************
[ARK SAID]
So what? You can not ANY differential geometry without contravariant
tensors. Remember, first you have tangent space (which are
contravariant vectors) and only THEN you define differential forms
as DUAL space. Some geometrical objects are vectors, some
are forms. Some are mixed objects. Don't you know all that?
[RMK SAYS]
BUT YOU CAN HAVE DIFFERENTIAL TOPOLOGY without contravariant tensors.
e.g. differential forms
For example, the anholonomic constraint F-dA = 0
as stated in terms of differential forms
on variety of any dimension
constrains the domain of support of F to be either open, or compact with
boundary.
It cannot be compact without boundary. (Gromov's theorem).
****
I have had a thorough training and many years experience in tensors and do
indeed recognize how they behave relative to diffeomorphic mappings.
***
BUT NOW FOR YOUR EDIFICATION:
Consider a map from say three dimensions into four. Let the map be
differentiable. Does the inverse Jacobian exist? Answer: NO.
I now give you a contravariant vector field on the three dimensional space
as
an ordered set of functions on the three independent variables.
Can you tell me the functional format of the contravariant vector field on
the 4 dimensional space? The answer is NO.
You can use the tensor transformation law and the computed non-square
Jacobian matrix to yield 4 component functions on the four dimensional
space.
But the arguments of these 4 functions are not in terms of the 4
independent
variables on the 4 D space. The arguments of the functions are still in
terms of the independent variables on the 3 D space!! As there
(generally)
is no inverse mapping, you cannot convert the arguments to variables on
the 4
D space.
YOU CANNOT (in general) tell me the functional form of the contra vector
on
the 4 space in terms of 4 functions that are defined on the 4 space via
the
Jacobian mapping, given a contra vector on 3 space.
Now, suppose I give you a differential 1-form on the 4 space with
covariant
coefficients whose arguments are the independent variables on the 4 space.
I
now pull back by functional substitution the differential form to the 3
space to yield a covariant set of three functional components. Can I tell
you the functional format of the three covariant functions with arguments
that are the independent variables on the 3 space? THE ANSWER IS YES!
This behavior demonstrates that differential forms on covariant fields
carry
more information that contravariant fields.
And that is why differential forms are (more) useful in differential
geometry
than contravariant tensors. It is also why Chern and others use the
differential form method of differential geometry as invented by Cartan.
*****
ARK may take contra tensors as the starting point, but I (and others) do
not.
The primitive more important objects are the differential forms, as they
are
functionally better behaved than contravariant tensors with respect to a
larger class of mappings.
I believe to state that first come contra vectors, and then differential
forms as "duals" is far to restrictive and slights the Cartan methods. Why
not take the opposite view and say that differential forms come first, and
then come contra vector (densities). This mechanism leads to well defined
functional forms under the rules of functional substitution, where the ARK
suggestion does not, unless the domains are restricted to diffeomorphisms.
Also note in projective spaces, the concept of a unit dual is meaningless.
Differential forms exist in projective spaces, but the concept of a unit
Tangent vector does not, as the projective space has no metric.
The facts that the second jet bundles (ARK did you read Libermann?) do not
form an intrinsic vector space on contravariants, but do form an intrinsic
vector space on the covariants should be convincing that something is
fundamentally different between the two species.
If you restrict yourself to diffeomorphisms, then the two species are
alias -
alibi equivalent, as the existence of an inverse mapping and an inverse
Jacobian allow you to transform one into the other in a functionally well
behaved manner. I am not interested in these situations. IMO the
diffeomorphism constraint is far too restrictive, and effectively
eliminates
the possibility of including thermodynamic irreversibility in a natural
way.
*****
IMO IT IS NOT NONSENSE that as I stated "Differential Geometry in terms of
differential forms has its advantages." I do not respect ARK's opinion
on
this point where he states with regard to my statement:
"NONSENSE - as Jack would say!"
It is also recognized that differential forms are important in other
areas.
I wish I could remember exactly what V. Arnold wrote. Something like
"...You
cannot fully understand Hamiltonian mechanics without knowledge of
differential forms" It is in a heading to one of his chapters in his book
on
mechanics, as I remember. I will look this up when I get access to a
library.
I respect the opinion of Marsden and Arnold.
IT appears to me that the use of differential forms yields an interesting,
novel and useful approach to problems of thermodynamic irreversibility,
problems that have not been solved heretofore by contravariant methods.
IMO Cartan's methods and cohomology are important methods of making
progress
in areas where other techniques have failed.
Regards
RMK
|
From: Laura Jadczyk-Knight
To: RKiehn2352atxaol.com
Subject: Re: Lorentz Force
Send reply to: wwwatxcassiopaea.com
Date sent: Sat, 4 Dec 1999 18:03:38 -0500
On 4 Dec 99, at 16:25, RKiehn2352atxaol.com wrote:
From: RKiehn2352atxaol.com
Date sent: Sat, 4 Dec 1999 16:25:06 EST
Subject: Re: Lorentz Force
To: wwwatxcassiopaea.com
Copies to: sarfattiatxwell.com, tephippsatxpdnt.com (Tom Phipps)
> Hi
> I DO NOT say that the LORENTZ force has anything to do with dU
You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING.
> I have said that the Lorentz Force format has to do with the other part
> of
> the Cartan
You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING.
> formula describing the Lie derivative acting on differential forms.
> IT IS GENERATED by the term W-=i(V)dA NOT dU
> IT has nothing to do with dU!
You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING.
> Why do you keep trying to say that the LORENTZ force involves dU,
> I DO NOT SAY THAT --- THAT IS YOUR SPIN, not mine.
You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING.
> The crucial issue is that the format E + V x B is indeed deducible from
> the
> expression i(V)dA
It is not deducible. It is JUST THAT!
But: You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING.
> -- which ( I presume) you now concede is indeed part of the Lie derivative
> construction called Cartan's magic formula. L(V)A = i(V)dA + d(i(V)A)
> I suggest again that you read Marsden.
You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING.
> **************
> **************
> DO YOU AGREE or DISAGREE that the format
> E + VxB comes from i(V)dA.
> *************
It is not only deducible. It is JUST THAT!
But: You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING. Why? Because Lie derivative
has derivatives of V while Lorentz force has them not.
Therefore what you said is MISLEADING.
That is what I said. And that is what I am repeating
again and again: You said that LORENTZ force pops out from Lie
derivative.
I said that it is MISLEADING. Why? Because Lie derivative
has derivatives of V while Lorentz force has them not.
Therefore what you said is MISLEADING.
ark
|
From: RKiehn2352atxaol.com
Date sent: Sat, 4 Dec 1999 16:25:12 EST
Subject: Lorentz force again
To: wwwatxcassiopaea.com (Arkadiusz Jadczyk)
Copies to: sarfattiatxwell.com, tephippsatxpdnt.com (Tom Phipps)
Hi
I am sorry that I have misinterpreted what you have written to me.
But your hang up is now quite clear. as repeated below.
[ARK SAID about 7times]
It has nothing to do with Lorentz force and with problem at hand, which
is
whether Lie derivative is relevant for this or not.
[RMK says - ]
I refuse to submit to propaganda
(- a repeated use of the same words until they are believed as gospel)
It can be demonstrated that the format of the Lorentz force
is deducible from the non - exact part of the definition of the
Lie derivative acting on forms.
Counter to ARKS prejudice and opinion, the mathematics is
conclusive and can be replicated by anyone (who is willing to try)
As the technique I suggest can be replicated by others,
where the format of the Lorentz force indeed can be obtained by the use
of the Lie derivative applied to differential formsm, I leave to the
reader
to conclude whether or not this is not a useful mechanism.
[ARK also SAID
... re to the fact that the behavior of contravariants and covariants
behave
differently under continuous mappings.]
Sure. But it is not little recognized. It is the FIRST thing that
you learn in differential geometry.
[RMK says]
I was taught differential geometry by Dirk Struik at MIT,
admittedly a long time ago and it is my experience that your statement is
not
true.
In addition, I have read most of the text books that have come out over
the
years
about Differential Geometry in order to keep up.
You learn about diffeomorphic differential geometry,
which involves the classic restrictions of tensor analysis. You learn
that
contravariants transform as the JAcobian and covariants transform as the
JAcobian inverse. However you do not (generally) learn how to deal with
transformations where the JAcobian inverse does not exist.
That is,you are not taught how to deal with non-homeomorphic maps.
****
However, you have your opinion to which I can NOT agree.
***
In Physics, I do not believe that it is possible to make a measurement
that
can distinguish an evolutionary difference in intrinsic behavior between
covariants and contravariants, if the experiment does not involve
irreversible dissipation. In other words, evolutionary measurements of
conservative reversible approximations yield result for contravariant
tensors
that can be mapped into covariant tensors uniquely, as the map and its
Jacobian exist and the inverses of both exist. This is not true for
continuous maps that admit jacobians that are not invertible and do not
have
unique inverse. It is the remarkable result of the pullback concept that
the
covariant differential forms are well behaved (contravariants are not) in
that by functional substitution techniques the preimage is functionally
well
defined.
I gather you did not read
http://www22.pair.com/csdc/pdf/retrodic.pdf
Regards
RMK
|
From: Laura Jadczyk-Knight
To: RKiehn2352atxaol.com
Subject: Re: Lorentz force again
Send reply to: wwwatxcassiopaea.com
Date sent: Sat, 4 Dec 1999 18:17:12 -0500
On 4 Dec 99, at 16:25, RKiehn2352atxaol.com wrote:
From: RKiehn2352atxaol.com
Date sent: Sat, 4 Dec 1999 16:25:12 EST
Subject: Lorentz force again
To: wwwatxcassiopaea.com (Arkadiusz Jadczyk)
Copies to: sarfattiatxwell.com, tephippsatxpdnt.com (Tom Phipps)
> Hi
> I am sorry that I have misinterpreted what you have written to me.
> But your hang up is now quite clear. as repeated below.
>
> [ARK SAID about 7times]
> It has nothing to do with Lorentz force and with problem at hand, which is
> whether Lie derivative is relevant for this or not.
>
> [RMK says - ]
> I refuse to submit to propaganda
> (- a repeated use of the same words until they are believed as gospel)
>
> It can be demonstrated that the format of the Lorentz force
> is deducible from the non - exact part of the definition of the
> Lie derivative acting on forms.
You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING. Why? Because Lie derivative
has derivatives of V while Lorentz force has them not.
Therefore what you said is MISLEADING.
> Counter to ARKS prejudice and opinion, the mathematics is
> conclusive and can be replicated by anyone (who is willing to try)
You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING. Why? Because Lie derivative
has derivatives of V while Lorentz force has them not.
Therefore what you said is MISLEADING.
> As the technique I suggest can be replicated by others,
> where the format of the Lorentz force indeed can be obtained by the use
> of the Lie derivative applied to differential formsm, I leave to the reader
> to conclude whether or not this is not a useful mechanism.
You said that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING. Why? Because Lie derivative
has derivatives of V while Lorentz force has them not.
Therefore what you said is MISLEADING.
> [ARK also SAID
> ... re to the fact that the behavior of contravariants and covariants behave
> differently under continuous mappings.]
> Sure. But it is not little recognized. It is the FIRST thing that
> you learn in differential geometry.
>
> [RMK says]
>
> I was taught differential geometry by Dirk Struik at MIT,
> admittedly a long time ago and it is my experience that your statement is not
> true.
Well, maybe at MIT they do not really know much about differential
geometry. Maybe they do not teach there about covariant and
contravariant functors. So, I am ready to fix my statement:
"It is the FIRST thing that you learn in any good course of
differential geometry."
> In addition, I have read most of the text books that have come out over the
> years
> about Differential Geometry in order to keep up.
> You learn about diffeomorphic differential geometry,
> which involves the classic restrictions of tensor analysis. You learn that
> contravariants transform as the JAcobian and covariants transform as the
> JAcobian inverse. However you do not (generally) learn how to deal with
> transformations where the JAcobian inverse does not exist.
You mean non-differentiable transformations? Then you do not know
how to pull back differential forms either. You do not know how to
pull back differentiable functions either.
> That is,you are not taught how to deal with non-homeomorphic maps.
I hope what you wrote now is a missprint rather that you really
wanted to write it. non-honeomorphic means either non 1-1
or non-continuous or both. What do you mean? I have no
idea. Because above you were talking about
non-existence of Jacobian. Jacobian always exists for
a differentiable map, even if it is non-homeomorphic, that
is even if it is not 1-1. So, what really you want tyo convey?
> However, you have your opinion to which I can NOT agree.
> ***
Which is my opinion that do not agree with?
> In Physics, I do not believe that it is possible to make a measurement that
> can distinguish an evolutionary difference in intrinsic behavior between
> covariants and contravariants, if the experiment does not involve
> irreversible dissipation. In other words, evolutionary measurements of
> conservative reversible approximations yield result for contravariant tensors
> that can be mapped into covariant tensors uniquely, as the map and its
> Jacobian exist and the inverses of both exist. This is not true for
> continuous maps that admit jacobians that are not invertible and do not have
> unique inverse. It is the remarkable result of the pullback concept that the
> covariant differential forms are well behaved (contravariants are not) in
> that by functional substitution techniques the preimage is functionally well
> defined.
This has nothing to do with our problem at hand, which is that
stating that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING. Why? Because Lie derivative
has derivatives of V while Lorentz force has them not.
Therefore what you said was MISLEADING.
> I gather you did not read
> http://www22.pair.com/csdc/pdf/retrodic.pdf
This has nothing to do with our problem at hand, which is that
stating that LORENTZ force pops out from Lie derivative.
I said that it is MISLEADING. Why? Because Lie derivative
has derivatives of V while Lorentz force has them not.
Therefore what you said was MISLEADING.
Best,
ark
|
From: RKiehn2352@aol.com
Date sent: Sun, 5 Dec 1999 11:37:24 EST
Subject: Lorentz Force AGAIN!
To: wwwatxcassiopaea.com(Arkadiusz Jadczyk)
Copies to: sarfattiatxwell.com, tephippsatxpdnt.com (Tom Phipps)
ARK
You are more stubborn than my Polish gradfather.
However, the issue ends here as I am willing to let the readers decide.
I believe things are summarized at
RMK - ARK on Lorentz Force
I have my opinion that differential topology is significant and its
applications should be encouraged. The idea that Cartan's formula for the
Lie derivative acting on forms yields the functional format for the
Lorentz force as a component of the Lie derivative is mathematically
correct. You seem to feel that this is misleading and I do not. Regards
RMK
|