

Next: 6. Continuous part of
Up: 4. Notes
Previous: 4. Geometrical meaning of
Our algorithm is, in
fact, a version of a nonlinear iterated function system
(IFS).
Figure:
The classical fractal: Sierpinski Triangle generated by an Iterated Function System.
|
|
Such algorithms are known to produce complex geometrical
structures by repeated application of several non-commuting affine
maps. The best known example is the Sierpinski triangle
generated by random application of 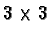 matrices
matrices ![$A[i],
i=1,2,3$](/quantum_future/papers/qfract/img147.gif) to the vector:
to the vector:
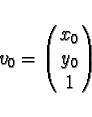 |
(21) |
where ![$A[i]$](/quantum_future/papers/qfract/img149.gif) is given by
is given by
![\begin{displaymath}
A[i]=\pmatrix{0.5&0&ax_i\cr 0&0.5&ay_i\cr0&0&1}
\end{displaymath}](/quantum_future/papers/qfract/img150.gif) |
(22) |
and
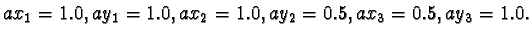 (Our
(Our 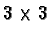 matrices encode affine transformations -
usually separated into a
matrices encode affine transformations -
usually separated into a 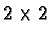 matrix and a translation
vector.) At each step one of the three transformations
matrix and a translation
vector.) At each step one of the three transformations ![$A[i],
i=1,2,3$](/quantum_future/papers/qfract/img147.gif) is selected with probability
is selected with probability ![$p[i]=1/3$](/quantum_future/papers/qfract/img152.gif) . After each
transformation the transformed vector is plotted on the
. After each
transformation the transformed vector is plotted on the 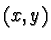 plane. Theoretical papers on IFSs usually assume that the system
is hyperbolic that is that each transformation is a
contraction, i.e. the distances between points get smaller and
smaller. It was shown in [17] that this assumption can
be essentially relaxed when transformations are non-linear and act
on a compact space - as is in the case of quantum fractals we are
dealing with.
plane. Theoretical papers on IFSs usually assume that the system
is hyperbolic that is that each transformation is a
contraction, i.e. the distances between points get smaller and
smaller. It was shown in [17] that this assumption can
be essentially relaxed when transformations are non-linear and act
on a compact space - as is in the case of quantum fractals we are
dealing with.


Next: 6. Continuous part of
Up: 4. Notes
Previous: 4. Geometrical meaning of
2002-04-11
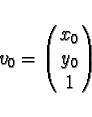
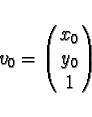
![\begin{displaymath}
A[i]=\pmatrix{0.5&0&ax_i\cr 0&0.5&ay_i\cr0&0&1}
\end{displaymath}](/quantum_future/papers/qfract/img150.gif)