

Next: 2. The algorithm
Up: 2. EEQT - Quantum
Previous: 2. EEQT - Quantum
We have published, as an OpenSource project
the algorithm implemented in Java that generates the Five Platonic
Fractals - that is fractals generated by five most symmetric
detector configurations. The algorithm generates self-similar
patterns on a sphere of a unit radius. The points on the sphere
represent (pure) states of the simplest quantum system - the spin
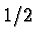 rotator. This spin
rotator. This spin 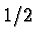 quantum system is coupled,
continuously in time, to a finite number of symmetrically
distributed spin-direction detectors. Thus the symmetry of the
pattern reflects the symmetry of the detector directions
distribution. Each spin direction is characterized by a vector
quantum system is coupled,
continuously in time, to a finite number of symmetrically
distributed spin-direction detectors. Thus the symmetry of the
pattern reflects the symmetry of the detector directions
distribution. Each spin direction is characterized by a vector
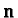 of unit length. Here we study most symmetrical
configurations, therefore we chose direction vectors
of unit length. Here we study most symmetrical
configurations, therefore we chose direction vectors 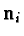 pointing from the origin to the vertices of one of the five
platonic solids. We consider the following five detectors
configurations:
pointing from the origin to the vertices of one of the five
platonic solids. We consider the following five detectors
configurations:![[*]](/quantum_future/papers/qfract/foot_motif.gif)
- tetrahedron: 4 detectors along the directions
![${\bf n}[i], i=1,\ldots ,4$](/quantum_future/papers/qfract/img6.gif)
{{0, 0, 1.}, {a[17], 0, -a[3]}, {-a[6],
a[12], -a[3]},
{-a[6], -a[12], -a[3]}}
- octahedron: 6 detectors along the directions
![${\bf n}[i], i=1,\ldots ,6$](/quantum_future/papers/qfract/img7.gif)
{{0, 0, 1.}, {1., 0, 0}, {0, 1., 0},
{-1., 0, 0}, {0, -1., 0}, {0, 0, -1.}}
- cube: 8 detectors along the directions
![${\bf n}[i], i=1,\ldots ,8$](/quantum_future/papers/qfract/img8.gif)
{{0, 0, 1.}, {a[17], 0, a[3]}, {-a[6], a[12],
a[3]},
{-a[6], -a[12], a[3]},
{a[6],
a[12], -a[3]}, {a[6], -a[12], -a[3]},
{-a[17],
0, -a[3]}, {0, 0, -1.}}
- icosahedron: 12 detectors along the directions
![${\bf n}[i], i=1,\ldots ,12$](/quantum_future/papers/qfract/img9.gif)
{{0, 0, 1.}, {0.a[15], 0, a[5]}, {a[2], a[13],
a[5]},
{-a[10], a[7], a[5]},
{-a[10], -a[7],
a[5]}, {a[2], -a[13], a[5]},
{a[10],
a[7], -a[5]},
{a[10], -a[7], -a[5]},
{-a[2],
a[13], -a[5]}, {-a[15],
0, -a[5]},
{-a[2], -a[13], -a[5]},
{0, 0, -1.}}
- dodecahedron: 20 detectors along the directions
![${\bf n}[i], i=1,\ldots ,20$](/quantum_future/papers/qfract/img10.gif)
{{0, 0, 1.}, {a[9], 0, a[11]}, {-a[3], a[8],
a[11]}, {-a[3], -a[8], a[11]},
{a[11], a[8],
a[3]}, {a[11], -a[8], a[3]}, {-a[14], a[4],
a[3]},
{a[1], a[16], a[3]}, {a[1], -a[16],
a[3]}, {-a[14], -a[4], a[3]},
{a[14],
a[4], -a[3]}, {a[14], -a[4], -a[3]}, {-a[11],
a[8], -a[3]},
{-a[1],
a[16], -a[3]}, {-a[1], -a[16], -a[3]}, {-a[11], -a[8], -a[3]},
{a[3],
a[8], -a[11]}, {a[3], -a[8], -a[11]}, {-a[9],
0, -a[11]},
{0, 0, -1.}}
where the array of real numbers
![$a[i],\/ i=1,\ldots ,17$](/quantum_future/papers/qfract/img11.gif) is given
in the following table.
is given
in the following table.


Next: 2. The algorithm
Up: 2. EEQT - Quantum
Previous: 2. EEQT - Quantum
2002-04-11
![[*]](/quantum_future/papers/qfract/foot_motif.gif)
![$a[1]=\frac{3-\sqrt{5}}{6}$](/quantum_future/papers/qfract/img12.gif)
![$a[2]=\frac{5-\sqrt{5}}{10}$](/quantum_future/papers/qfract/img13.gif)
![$a[4]=\frac{\sqrt{5}-1}{2\sqrt{3}}$](/quantum_future/papers/qfract/img15.gif)
![$a[6]=\frac{\sqrt{2}}{3}$](/quantum_future/papers/qfract/img17.gif)
![$a[7]=\sqrt{\frac{5-\sqrt{5}}{10}}$](/quantum_future/papers/qfract/img18.gif)
![$a[10]=\frac{5+\sqrt{5}}{10}
$](/quantum_future/papers/qfract/img21.gif)
![$a[11]=\frac{\sqrt{5}}{3}$](/quantum_future/papers/qfract/img22.gif)
![$a[12]=\sqrt{\frac{2}{3}}$](/quantum_future/papers/qfract/img23.gif)
![$a[13]=\sqrt{\frac{5+\sqrt{5}}{10}}$](/quantum_future/papers/qfract/img24.gif)
![$a[14]=\frac{3+\sqrt{5}}{6}$](/quantum_future/papers/qfract/img25.gif)
![$a[16]=\sqrt{\frac{3+\sqrt{5}}{6}}$](/quantum_future/papers/qfract/img27.gif)
![$a[17]=\frac{2\sqrt{2}}{3}$](/quantum_future/papers/qfract/img28.gif)