

Next: 4. Notes
Up: 3. The Five Platonic
Previous: 5. Dodecahedron
In principle our algorithm should create quantum fractals for each
of the regular polyhedra. The only restriction on the array of
vectors ![${\bf n}[i]$](/quantum_future/papers/qfract/img109.gif) is that they are all of unit length, and their sum
is a zero vector. We added, for comparison with the Platonic
solids configurations, two additional simple yet regular figures:
double tetrahedron and icosidodecahedron. Notice that tetrahedron
is self-dual, while dodecahedron and icosahedron are dual to each
other. Double tetrahedron array is obtained by combining
is that they are all of unit length, and their sum
is a zero vector. We added, for comparison with the Platonic
solids configurations, two additional simple yet regular figures:
double tetrahedron and icosidodecahedron. Notice that tetrahedron
is self-dual, while dodecahedron and icosahedron are dual to each
other. Double tetrahedron array is obtained by combining ![${\bf n}[i]$](/quantum_future/papers/qfract/img109.gif) with
with ![$-{\bf n}[i]$](/quantum_future/papers/qfract/img110.gif) - that is with the inverted configuration.
- that is with the inverted configuration.
Figure:
Quantum Double Tetrahedron. 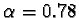
|
|
Icosidodecahedron has particularly simple and elegant expression
for its 30 vertices: they are of the form: 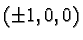 and its
cyclic permutations, and
and its
cyclic permutations, and
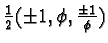 and its cyclic permutations, where
and its cyclic permutations, where
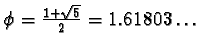 is the golden ratio.
All of its edges are of length
is the golden ratio.
All of its edges are of length 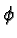 . For its 30 vertices
. For its 30 vertices
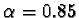 was needed to resolve the atrractor's fine
structure.
was needed to resolve the atrractor's fine
structure.
Figure:
Quantum Icosidodecahedron. 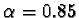
|
|


Next: 4. Notes
Up: 3. The Five Platonic
Previous: 5. Dodecahedron
2002-04-11
![\includegraphics [width=11cm, keepaspectratio=true]{q_double_tetrahedron_07c.eps}](/quantum_future/papers/qfract/img111.gif)
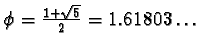 is the golden ratio.
All of its edges are of length
is the golden ratio.
All of its edges are of length