

Next:EEQT:
FAQUp:EEQT
- a few Previous:node5.html
In EEQT it is possible to model a simulataneous measurement of several
non-commuting observables. And example would be a simultaneous measurement
of the same component of position an momentum. This case, however, has
not yet been studied - because of its computational difficulties. A simpler
problem, namely that of a simultaneous measurement of several spin projections
leads to chaotic behavior and fractal structure on the space of pure states.
Following the discussion given in [33]
let us couple a spin 1/2 quantum system to four yes-no polarizers corresponding
to spin directions 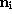 , i=0,1,2,3, arranged at the vertices of a regular tetrahedron.
Choosing the same coupling structure
, i=0,1,2,3, arranged at the vertices of a regular tetrahedron.
Choosing the same coupling structure  for all four polarizers the model leads to a homogeneous (in time) Poisson
process on the sphere
for all four polarizers the model leads to a homogeneous (in time) Poisson
process on the sphere 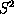 of norm 1 quantum spin states. The process is a non-linear version of Barnsley's
iterated function system [32] and can be
described as follows:
of norm 1 quantum spin states. The process is a non-linear version of Barnsley's
iterated function system [32] and can be
described as follows:
for i=0,1,2,3 let 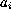 be the 2 by 2 matrices
be the 2 by 2 matrices 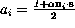 , where
, where  are the Pauli matrices, and let
are the Pauli matrices, and let 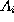 be the four operators acting on
be the four operators acting on 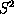 by
by 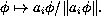 These operators play the role of Barnsley's affine transformations. To
each transformation there is associated probability
These operators play the role of Barnsley's affine transformations. To
each transformation there is associated probability 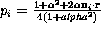 , where
, where  is the radius-vector of the actual point on the spehere, that is to be
transformed. Iteration leads to a self-similar structure, with sensitive
dependence on the initial state and on the value of the coupling constant.
Numerical simulation shows that when
is the radius-vector of the actual point on the spehere, that is to be
transformed. Iteration leads to a self-similar structure, with sensitive
dependence on the initial state and on the value of the coupling constant.
Numerical simulation shows that when  decreases from 0.95 to 0.75, Hausdorff dimension of the limit set increases
from 0.5 to 1.3. Fig. 1 shows a typical picture -
here for
decreases from 0.95 to 0.75, Hausdorff dimension of the limit set increases
from 0.5 to 1.3. Fig. 1 shows a typical picture -
here for 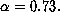 For details see [34].
For details see [34].
Converted to HTML by Robert Coquereaux
Tue Dec 29 10:54:13 WET 1998