Let us consider the simplest case: that of a two-state classical system. We call its two states "off" and "on." Its action is simple: if it is off, then it will stay off forever. If it is on, then it can detect a particle and go off. Later on we will specialize to detection of particle presence at a given location in space. For a while let us be general and assume that we have two Hilbert spaces and two Hamiltonians . We also have a time dependent family of operators and let us denote . According to the theory presented in the previous section, with , , the master equation for the total system, i.e. for particle and detector, reads:

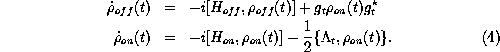
Suppose at t=0 the detector is "on" and the particle state is , with Then, according to the event generating algorithm described in the previous section, probability of detection during time interval (0,t) is equal to

Let us now specialize and consider a detector of particle present at a location a in space (of n dimensions). Our detector has a certain range of detection and certain efficiency. We encode these detector characteristics in a gaussian function:

If the detector is moving in space along some trajectory a(t), and if the detector characteristics are constant in time, then we put: . Let us suppose that the detector is off at and that the particle wave function is . Then, according to the algorithm described in the previous section, probability of detection in the infinitesimal time interval equals . In the limit , when we get . Thus we recover the usual Born interpretation, with the evident and necessary correction that the probability of detection is proportional to the length of exposure time of the detector.
That simple formula holds only for short exposure times. For a prolonged detection, the formula becomes more involved, primarily because of non-unitary evolution due to the presence of the detector. In that case, numerical simulation is necessary. To get an idea of what happens, let us consider a simplified case which can be solved exactly. We will consider the ultra-relativistic Hamiltonian H=-i d/dx in space of one dimension. In that case the non-unitary evolution equation is easily solved:

In the limit when the detector shrinks to a point, and assuming that this point is fixed in space a(t)=a, we obtain for the probability p(t) of detecting the particle in the time interval (0,t):

Intuitively this result is very clear. Our Hamiltonian describes a particle moving to the right with velocity c=1, the shape of the wave packet is preserved. Then p(t) is equal to the probability that the particle at t=0 was in a region of space that guaranteed passing the detector, multiplied by the detector efficiency factor - in our case this factor is