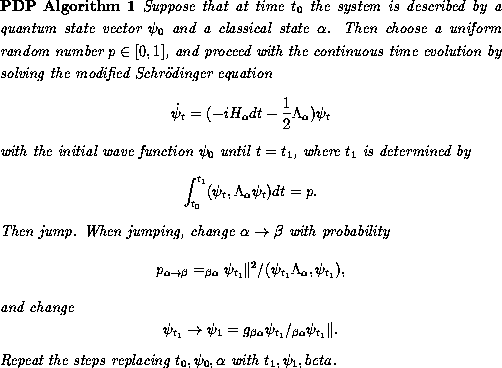There are two levels of EEQT - the ensemble level and the individual level.
Let us consider first the ensemble level.
First of all, in EEQT, at that level, we use all the standard mathematical formalism of quantum
theory, but we extend it adding an extra parameter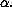 
Thus
all quantum operators A get an extra index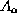 
, quantum
Hilbert space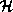 
is replaced by a family 
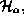quantum state vectors 
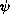are replaced by families 
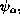quantum Hamiltonian H is replaced by a family 
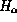etc.
The parameter 
is used to distinguish between macroscopically
different and non-superposable states of the universe. In the simplest
possible model we are interested only in describing a "yes-no" experiment
and we disregard any other parameter - in such a case will have
only two values 0 and 1. Thus, in this case, we will need two Hilbert
spaces. This will be the case when we will deal with particle detectors.
In a more realistic situation will take values in a
multi-dimensional, perhaps even infinite-dimensional manifold - like,
for instance, in a phase space of a tensor field. But even that may
prove to be insufficient. When, for instance, EEQT is used as an engine
powering Everett-Wheeler many-world branching tree, in that case
alpha will also have to have the corresponding dynamical branching tree structure, where the space in which the parameter takes
values, grows and becomes more and more complex together with the growing complexity of the branching structure.
An event is, in our mathematical model, represented by a change of
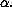This change is discontinuous, is a branching. Depending on
the situation this branching is accompanied by a more or less radical
change of physical parameters. Sometimes, like in the case of a phase
transition in Bose-Einstein condensate, we will need to change the
nature of the underlying Hilbert space representation. In other cases,
like in the case of a particle detector, the Hilbert spaces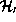 
and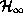 
will be indistinguishable copies of one standard
quantum Hilbert space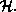 
A second important point is this: time evolution of an individual quantum system is described by piecewise continuous function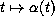 
,
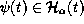, a trajectory of a piecewise deterministic
Markov process. The very concept and the theory of piecewise deterministic processes (in short: PDP) is not a part of the standard mathematical education, even for professional probabilists. But the point is that it is impossible to
unerstand the essence of EEQT without having even a rough idea about PDPs.
Originally EEQT was described in terms of a master equation for a coupled,
quantum+classical, system. Thus it was only applicable to ensambles - the question
of how to describe individual systems was open. Then, after searching through
the mathematical literature, we found that in his
monographs [37, 38]
dealing with stochastic control and optimization
M. H. A. Davis, having in mind mainly queuing and insurance models,
described a special class of piecewise deterministic
processes that fitted perfectly the needs of quantum
measurement theory, and that reproduced the master equation postulated
originally by us in [16].
It took us another couple of years to show [26] that the special
class of couplings between a
classical and quantum system leads to a unique piecewise deterministic
process with values on E-the pure state space of the total system.
That process consists of random jumps, accompanied by changes of a
classical state, interspersed by random periods of Schrödinger-type
deterministic evolution. The process, although mildly nonlinear in quantum
wave function 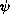, after averaging,
recovers the original linear master equation for statistical states.
It should be stressed that in EEQT
the dynamics of the coupled total system which is being modelled
is described not only by a Hamiltonian 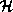, or better: not
only by an - parametrized family of Hamiltonians ,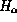
but also by a doubly parametrized family of operators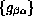 
,
where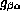 
is a linear operator from 
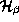to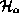 
. While Hamiltonians must be essentially self-adjoint,
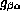need not be such - although in many cases, when information transfer and control is our concern (as in quantum computers), one wants them to be even positive operators (otherwise unnecessary entropy is created). This aspect of EEQT is rather difficult to accept
for a newcomer, as the first question he will ask is "where do we take
these operators from?" Our answer, elaborated in more details in FAQ-s
- see Section 5 - amounts to this: we find the correct operators
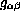the same way we find the correct Hamiltonians:
by trial and error! Each new solved model is a lesson and, little
by little, we learn more and more, and we aspire for more. As already said,
more on this subject in our FAQs section.
It is to be noted that the time
evolution of statistical ensembles is due to the presence of 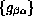's,
non-automorphic. The system, as a whole, is open. This is necessary, as we like
to emphasize: information (in this case: information gained by the classical
part) must be paid for with dissipation! The appropriate mathematical formalism
for discussing the ensemble level is that of completely positive semigroups,
as discussed by Kossakowski et al. [27], Lindblad [28]
and generalized so as to fit our purpose by Arveson [29] and
Christensen [30].
A general form of the linear master equation describing statistical evolution
of the coupled system is given by
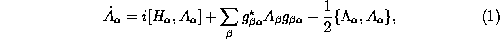
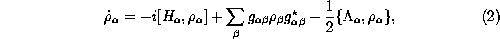
where
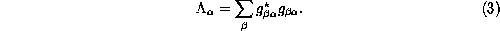
The operators 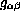can be allowed to depend explicitly
on time. While the term with the Hamiltonian describes "dyna-mics",
that is exchange of forces,
of the system, the term with 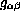describes its "bina-mics" -
that is exchange of "bits of information" between the quantum and the classical
subsytem.
As has been proven in [26] the above Liouville equation,
provided the diagonal terms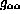 
vanish, can be
considered as an average of a unique Markov process governing the
behavior of an individual system.
The real-time behavior of such an individual system is given by a
PDP process realize by the following
non-linear and non-local, EEQT algorithm:
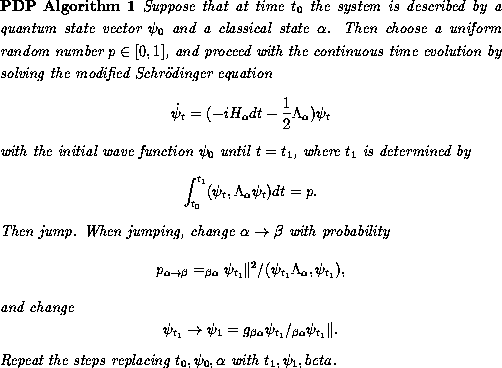
The algorithm is non-linear, because it involves repeated normalizations. It is non-local because it needs repeated computing of the norms - they involve space-integrations. It is to be noted that PDP processes are more general than the popular diffusion processes. In fact, every diffusion process can be obtained as a limit of a family of PDP processes.
