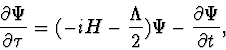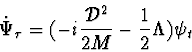Published in Foundations of Physics, 26 (1996) 1669-1691
 

Relativistic Quantum Events.

Ph. Blanchard 1and A. Jadczyk 2 1

1Faculty of Physics and BiBoS, University of Bielefeld
Universitätstr. 25, D-33615 Bielefeld
2Institute of Theoretical Physics, University of Wroclaw
Pl. Maxa Borna 9, PL-50 204 Wroclaw

Abstract:

Standard Quantum Theory is inadequate to explain the mechanisms by which potential becomes actual. Is inadequate and therefore unable to describe generation of events. Niels Bohr emphasized long ago that the classical part of the world is necessary. John Bell stressed the same point: that ``measurement" cannot even be defined within the Standard Quantum Theory, and he sought a solution within hidden variable theories and his concept of ``beables."
Today it is customary to try to explain emergence of the classical world through a decoherence mechanism due to ``environment". But, we believe, as it was with the concept of measurement, ``environment" itself cannot be defined within the Standard Quantum Theory.
We have proposed a semi-phenomenological solution to this problem by introducing explicitly, from the very beginning, classical degrees of freedom, and by coupling these degrees of freedom, through a Lindblad type coupling, to the quantum world. The resulting theory, we call ``Event Enhanced Quantum Theory". EEQT allows us to describe an event generating mechanism for individual quantum systems under continuous observation. The objections of John Bell are met and precise definitions of an ``experiment" and of a ``measurement" have been given within EEQT. However EEQT is, essentially, a non-relativistic theory.
In the present paper we extend the ideas of L.P. Horwitz and C. Piron and we propose a relativistic version of EEQT, with an event generating algorithm for spin one-half particle detectors. The algorithm is based on proper time formulation of the relativistic quantum theory. Although we use indefinite metric, all the probabilities controlling the random process of the detector clicks are non-negative.

1. Introduction.

Quantum Theory has significantly changed our perspective on what Reality truly is. Prior to Bohr and Heisenberg, speculations about Reality were in the domain of philosophy and not of physics. For a physicist, it was clear that there was a Reality ``out there", and that physics was about making as precise a description of this reality as possible. This Reality had two kinds of concepts connected to it: static concepts and dynamic concepts. Static concepts were ``objects," ``properties" of these objects, and ``relations" between the objects. Dynamic concepts were those of ``events"; defined as ``changes of property," or ``changes of relation." And, ``change" was understood as ``change in time".

With the advent of Quantum Theory the existence of this kind of simple reality was first questioned and later denied. Even if quantum physicists still used the concept of an ``object," it was no longer possible to speak about the actual properties and relations of said objects. A fortiori ``events" also disappeared from the vocabulary of quantum theory. Instead of objects and events, another concept emerged as the dominant idea - that of ``measurement" or ``observation".

There were however, physicists who were not dominated by the new idea. Some of them, the most prominent ones in this camp being Albert Einstein and David Bohm, believed that quantum theory is a temporary statistical description of some complex nonlinear substructure - yet to be identified. But opposition also appeared in Quantum Theory's own camp.

John A. Wheeler stressed repeatedly [1]: ``No elementary quantum phenomenon is a phenomenon until it is a registered (``observed," ``indelibly recorded") phenomenon." But, he did not give a definition of ``being recorded" - and we now understand why? Because such a definition could not be given within the orthodox quantum theory.

John Bell [2,3] was the first to clearly realize that the concepts of ``measurement" and ``observation" were being used in Quantum Theory to brainwash physicists into believing that these concepts are a part of Quantum Theory, while in reality they belong to a metastructure. He had the courage to say [4]: ``Either the wave function is not everything or it is not right..." and he opted for an extended theory that would contain, in addition to the quantum wave function, classical variables, which he termed ``beables" - for ``being able to be" [5].

These theories were, however, inconsistent. The classical part was acted upon (by the wave function) but there was no back reaction. There was thus no way to falsify these theories as no new results were predicted that would go beyond those predicted by the textbook recipes of the standard quantum theory.

It is our opinion that ``events" are classical in nature. They obey the classical ``yes-no" decision logic. Even if the decisions are based on fuzzy criteria - they are always sharp ``yes-no" decisions. They are points at which choices are being made. Those who adhere to the Many World Interpretation [6] would say: they are points at which the Universe splits into branches. Until we understand the true nature of quantum theory and the true nature of time, these choices must be considered as irreversible. What was done in the past cannot be undone later on.

In a series of papers (see [7] and references there) we have developed a semi-phenomenological theory of events - Event Enhanced Quantum Theory (EEQT). The theory is based on the linear time of Galileo and Newton. It is a theory of a special kind of irreversible coupling between quantum and classical systems. 2 Events are defined in this theory as changes of state of the classical subsystem. They are accompanied by quantum jumps - discrete changes of the quantum state. In this theory, the Schrödinger equation is replaced by a piecewise deterministic algorithm that simulates the behavior of an individual quantum system coupled to a classical ``measuring device".

We believe that the fundamental laws of Nature, that is the laws that Nature herself uses while producing the events of the world ``out there," are based on algorithms rather than on differential equations. These algorithms are discrete and probabilistic. The latter property mirrors the fact that we have to describe an infinitely complex universe with the finite means that are, at present, at our disposal.

A brief description of EEQT will be given in the the following Section. The simplest model that can be taken as an example for building more sophisticated ones is the cloud chamber model developed in [12,13]. It describes an irreversible coupling between a nonrelativistic quantum particle and an arbitrary number of detectors sensitive to the presence of the particle in localized areas of space.

From the very moment EEQT was born, we were aware of the unavoidable difficulties that might arise when the nonrelativistic theory would have to be replaced by one that is in agreement with Einstein's Relativity. The difficulties to be addressed in any attempt at building a relativistic theory of quantum measurement have long been known by the experts. (see [14], and for a recent discussion [15]). In a recent paper [16] we anticipated that the solution to this problem would have to involve algorithms that are non-local not only in space but also in time: ``However, if you try to work out a relativistic cloud chamber model (...) the events must be also smeared out in the coordinate time. (...). Nevertheless they can still be sharp in a different ``time", called ``proper time" after Fock and Schwinger." The proper time model of the cloud chamber is presented in Section 3. We have chosen relativistic spin ${1\over2}$ particle, as its proper-time quantum dynamics seems to cause more problems than spin $0$ case - this due to the lack of Lorentz invariant positive definite scalar product in the spin space. Our solution, presented in Section 3, consists of using positive detector coupling operators. In Section 2 we will recall the nonrelativistic detector model: its standard version, as discussed in Refs. [7,12,13,17], and also its ``proper time" version, so that a transition to the relativistic case is made easier.

2. Nonrelativistic Quantum Events.

We reiterate, together with John A. Wheeler: No elementary quantum phenomenon is a phenomenon until it is a registered phenomenon. And, physics is about phenomena. The goal of physics is to understand Nature's phenomena; to be able to construct an ``artificial Nature" much in the way the goal of biology is to be able to construct artificial life, the same way the ultimate goal of the computer sciences is to create artificial intelligence.

But to construct artificial Nature we must be able to reproduce, in terms of mathematical symbols, the natural phenomena. In order to do this we first must be able to define within mathematics what a phenomenon is. Or, more precisely, what a ``registered phenomenon" is. For this purpose, we will call an elementary registered phenomenon an event. And now we must define what constitutes an event in terms of the mathematical structure. We believe that it is obviously impossible to do this within the standard mathematical framework of the orthodox quantum theory. The framework must be extended, the theory must be enhanced. And, it so happens that the extension is, in fact, only a slight one. Significantly, nothing new is needed that has not already been discussed in the framework of a general algebraic quantum theory. The extension we have in mind consists of allowing algebraic quantities that are not in any kind of uncertainty relation to any other quantity, that is, allowing classical (in algebraic terms they are called ``central") quantities. In other words: a phenomenon can be registered, and an event can happen only if there is a classical subsystem of the given quantum system.

It could be said, strictly speaking, that in a pure quantum world nothing could or would ever ``happen." But we see that things do happen in the world out there. This creates an obvious contradiction. One possibility to get us out of the contradiction is to negate events and phenomena, to call them ``illusion," to admit only ``approximate events". This is the road that most quantum physicists of our day are prepared to take.

The other possibility is to accept that events do happen and to then introduce explicitly a classical subsystem. In this way, an event is defined as a change of state of this subsystem. This then gives us two further options. One option consists of admitting only mental events. That is to say, events do exist, they do happen, they are not illusions, but they happen only in mind. This is the option advocated by H. P. Stapp [18,19].

We are taking a less adventurous position by leaving the question ``what is truly and intrinsically classical?" open, or ``to be investigated." Therefore our theory, at the present stage, is semi-phenomenological. That is, we are building models that aim at reflecting some of the mechanisms of Nature, but which always can be improved by including more and more details in the description.

A general scheme of EEQT has been described in detail in Ref. [7] (see also [17] for a short version). Here we will specify the scheme to the particular but important case of a particle position detector. We must note that in the literature it is common to meet the opinion that any quantum measurement can be, in the last instance, reduced to position measurements. Although we do not share this conclusion, we believe that modelling particle position detectors is important and allows us to understand the mechanism through which other types of quantum phenomena are being registered as events.

2.1 Particle detectors

We consider a nonrelativistic particle on a line. When no detector is switched on then the quantum mechanical wave function $\Psi(x,t)$ representing the quantum state of the particle obeys the Schrödinger equation:

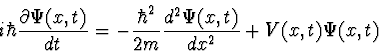
\begin{displaymath} i\hbar {{\partial\Psi(x,t)}\over{dt}}= -{{\hbar^2}\over{2m}} {{d^2\Psi(x,t)}\over {dx^2}} + V(x,t)\Psi(x,t) \end{displaymath} (1)

with a real potential $V(x,t)$. In particular the norm of the wave function is conserved. Now, according to our philosophy, the Schrödinger equation describes a continuous evolution of ``possibilities". Nothing happens. No phenomena. Now, let us add a particle detector that is coupled to the particle and can ``click" when the particle is ``nearby". How to describe the situation of the coupled pair particle+detector? The detector itself is idealized as a ``yes-no" device. As such it is a two-state classical system. For simplicity we will assume that the detector is at rest with respect to the coordinate system we are working in. When a quantum particle is coupled to a classical detector then we are dealing with a hybrid system. Its pure states are described by pairs $(\Psi,\alpha)$, where $\alpha=0,1$ describes the state of the detector. Statistical states of the total system are described by pairs $(\rho_0, \rho_1)$, where $\rho_\alpha$ is a positive operator in $L^2(R)$ such that $Tr (\rho_0)+ Tr(\rho_1)=1$. Now the coupling. We will consider here a detector that switches off after the first click and is no longer coupled to the particle. Other, more general types of particle detectors are described in the references quoted in [7]. The coupling is described by a positive operator $g$. For a particle detector that is sensitive to the particle position only, we will take for $g$ a function $g(x)\geq 0$ which describes its spatial sensitivity. One can think of $g(x)$ as a bell like function localized at the detector position. Thus for a point like detector the support of $g(x)$ would shrink to a single point. According to the general formalism of EEQT described briefly in Section 1.1 of Ref. [7] 3 the Liouville equation describing the time evolution of the statistical state of the total system reads:

$\displaystyle \left. \begin{array}{ll} {\dot \rho}_0&=-i[H,\rho_0]-{1\over2}\{\... ...,\rho_0\}, \\ &\\ {\dot \rho}_1&=-i[H,\rho_1]+g\rho_0 g, \end{array} \right\}$     (2)

where $\Lambda=g^2$. It follows from a general theorem proved in [20], that there is a unique Markov process on pure states of the total system that reproduces this evolution of ensembles. It is given by a piecewise deterministic algorithm (PDP of Ref. [7]) that governs the click time of the counter. In our case of a single counter the algorithm reads:

PDP Algorithm 1   Suppose that at time $t=0$ the system is described by a (normalized) quantum state vector $\psi_0$ and the counter is off: $\alpha=0$. Then choose a uniform random number $p_0\in [0,1]$, and proceed with the continuous time evolution by solving the modified Schrödinger equation
\begin{displaymath} {\dot \psi_t}=(-iH-{1\over2}\Lambda )\psi_t \end{displaymath} (3)

with the initial wave function $\psi_0$ until $t=t_1$, where $t_1$ is determined by

\begin{displaymath}\int_{0}^{t_1} (\psi_t,\Lambda \psi_t ) dt = p_0.\end{displaymath}

At $t=t_1$ the counter clicks, that is its state changes from $\alpha=0$ to $\alpha=1$ and, at the same time, the state vector jumps:

\begin{displaymath}\psi_{t_1}\rightarrow\psi_1=g\psi_{t_1}/ \Vert g\psi_{t_1}\Vert.\end{displaymath}

The evolution starts now again and it obeys the standard unitary Schrödinger equation with the Hamiltonian $H$ - until the counter starts its monitoring again, in which a case the continuous evolution becomes again described by Eq.(3), new random number $p_1$ is selected, and so on.

2.2 ``Proper time" formulation

In this subsection we will give a four-dimensional formulation of the nonrelativistic counter click model. It will essentially be just another formulation of the model above. We will see that in a certain limit it approximates the PDP algorithm of the previous subsection.

The Hilbert space we consider is now $L^2(R^2,dx dt)$ and the dynamics will be given by a ``super-Hamiltonian"

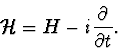
\begin{displaymath}{\cal H}=H-i{\partial\over{\partial}t}. \end{displaymath} (4)

There is an extra time parameter associated with the counter, we will denote it by $\tau$ and call it a ``proper time". The coupling between the quantum particle and the counter is described by a positive operator $G$ on our Hilbert space. The Liouville equation and the PDP algorithm are much the same as above except that $x$ is replaced by $(x,t)$ and $t$ is replaced by $\tau$.
Let us now see how this formalism includes one in the previous subsection. With the notation as in Sec. 1.1 let us take for the initial state $\Psi_0(x,t)$ a product:

\begin{displaymath} \Psi_0(x,t)=\phi(t)\psi_0(x), \end{displaymath} (5)

where $\phi(t)$ and $\psi(t)$ are square integrable (with respect to $dt$ and $dx$ respectively) of norm one, and $\Psi_0$ stands for $\Psi_{\tau=0}$. Let us assume that $G$ depends on $x$ only:

\begin{displaymath} G(x,t)=g(x). \end{displaymath} (6)

The equation (3) for $\psi(x,t)$ is now replaced by

\begin{displaymath} {{\partial\Psi}\over{\partial\tau}}=(-iH-{\Lambda\over 2})\Psi -{{\partial\Psi}\over{\partial t}}, \end{displaymath} (7)

which solves to:

\begin{displaymath} \Psi_\tau(x,t)=\phi(t-\tau ) e^{(-iH-{\Lambda\over2})\tau }\psi_0 (x). \end{displaymath} (8)

It is clear from this that identifying the coordinate time $t$ with the ``proper time" parameter $\tau$ we have the same inhomogeneous Poisson process governing the detector click as in the previous subsection.

Remark We have chosen the function $g$ to depend only on $x$ and not on time for the reason that in this case the operator $\Lambda$ commutes with $\partial/\partial t$, and so Eq. (7) is easily solved.

3. Relativistic Quantum Events.

Let us now consider the relativistic case. Proper time formulation of the relativistic quantum mechanics has been considered by many authors. We shall cite here the classical paper by Horwitz and Piron [21]. There are also two review papers, one by Kyprianidis [22], and one by Fanchi [23] (cf. also [24]), where more references can be found. While the case of spinless particle was relatively straightforward, the case of spin $1/2$ caused interpretational problems because of the lack of Lorentz invariant, positive definite, scalar product. Several possible ways out of this difficulty have been considered. Evans [25] proposes to accept the indefinite scalar product, while in [26,27,28,29] the authors introduce an additional superselection (classical) variable ${\bf n}$ to parametrize a family of positive definite scalar product Hilbert spaces. The latter was then discussed by Horwitz and Arshansky [30] who noticed that the Dirac operator was not Hermitian with respect to the positive definite products. Our model will use indefinite metric. In fact, according to our philosophy, there is no reason at all why scalar product is to be positive definite. This is because we do not start with the standard quantum mechanical probabilistic interpretation. We derive the interpretation from the coupling. So, the only thing that we have to worry about is that the probability of the detector click is to be non-negative. And we will see that this is indeed the case.
We will take the standard representation of gamma matrices:

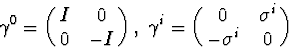
\begin{displaymath} \gamma^0=\pmatrix{I&0\cr0&-I\cr},\; \gamma^i=\pmatrix{0&\sigma^i\cr -\sigma^i&0\cr} \end{displaymath} (9)

and define an indefinite metric space by

\begin{displaymath} <\Psi , \Phi >=\int {\bar Psi}(x,t)\Phi(x,t) dx dt , \end{displaymath} (10)

where ${\bar\Psi}=\Psi^\dagger\gamma^0$ . The Dirac matrices are Hermitian with respect to this scalar product, and so is the Dirac operator:

\begin{displaymath} {\cal D}= i\gamma^\mu (\partial_\mu+ieA_\mu)-m . \end{displaymath} (11)

Let us consider now a particle position detector which, for simplicity, is at rest with respect to the coordinate system. We associate with it the operator $G$ defined by

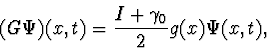
\begin{displaymath} (G\Psi)(x,t)={{I+\gamma_0}\over 2}g(x)\Psi(x,t), \end{displaymath} (12)

where $g(x)$ is a positive, bell-like, function centered over the detector position. 4 It follows now that $G$ is positive, Hermitian with respect to the indefinite metric scalar product, and the same holds for $\Lambda=G^2$. We postulate the following relativistic version of the PDP algorithm:

Relativistic PDP Algorithm 1   Suppose that at proper time $\tau=0$ the system is described by a quantum state vector $\Psi_0$ and the counter is off: $\alpha=0$. Then choose a uniform random number $p\in [0,1]$, and proceed with the continuous time evolution by solving the modified evolution equation


\begin{displaymath} {\dot \Psi}_\tau =(-i{{{\cal D}^2}\over{2M}}-{1\over2}\Lambda )\psi_t \end{displaymath} (13)

with the initial wave function $\Psi_0$ until $\tau=\tau_1$, where $\tau_1$ is determined by

\begin{displaymath}\int_{0}^{\tau_1} (\Psi_\tau ,\Lambda \Psi_\tau ) d\tau = p.\end{displaymath}

At $\tau=\tau_1$ the counter clicks, that is its state changes from $\alpha=0$ to $\alpha=1$ and, at the same time, the state vector jumps:

\begin{displaymath}\Psi_{\tau_1}\rightarrow\Psi_1=G\Psi_{\tau_1}/ <\Psi_{\tau_1},G\Psi_{\tau_1}>.\end{displaymath}

If, after the first click, the detector is deactivated, then after the click the evolution starts again and it obeys the standard unitary Schrödinger equation with the Hamiltonian ${\cal H} = \frac{D^2}{2M}$.

The algorithm contains second order, proper time, Dirac equation. This equation can be geometrically derived by the method of dimensional reduction along an isotropic Killing vector field in six dimensional space of signature $(++++,--)$ in an exact analogy to the derivation of Levy-Leblond and Pauli equation from five-dimensional space of signature $(++++,-)$ - cf. Ref. [31]. It is clear from the definition that the algorithm works well and can be repeated. Let us now assume that there are two detectors, both at rest with respect to the coordinate system. They are both coupled to the quantum particle, the coupling operators $G_i, i=1,2$ being given, as before, by:

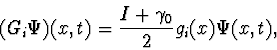
\begin{displaymath} (G_i\Psi)(x,t)={{I+\gamma_0}\over 2}g_i(x)\Psi(x,t), \end{displaymath} (14)

where the functions $g_i$ are localized at the detectors. The operator $\Lambda$ is now a sum of two contributions:

\begin{displaymath} \Lambda=G_1^2+G_2^2. \end{displaymath} (15)

The algorithm proceeds as before but now, when the event happens at $\tau=\tau_1$ a decision must be made which of the two detectors reacts. The probability $p_i$ that the $i$-th detector is activated is given by the same formula as in the nonrelativistic case (cf. Ref. [7] for a general theory):

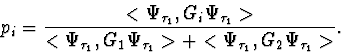
\begin{displaymath} p_i={{<\Psi_{\tau_1},G_i\Psi_{\tau_1}>}\over{ <\Psi_{\tau_1},G_1\Psi_{\tau_1}>+<\Psi_{\tau_1},G_2\Psi_{\tau_1}>}}. \end{displaymath} (16)

Generalization to a larger number of detectors, that are not necessarily at rest, is straightforward.

4. Final Remarks.

We have proposed a relativistic PDP algorithm that allows one to model the behavior of a detector coupled to a relativistic spin ${1\over2}$ particle. Adding more detectors does not cause any difficulties. Our algorithm is repeatable, thus allowing for a continuous monitoring of the particle position, as in the nonrelativistic cloud chamber model described in [12,13]. It would be interesting to see how our relativistic event generating algorithm can be used to test the idea of interference in time as discussed by Arshansky, Horwitz and Lavie in [32].

In the nonrelativistic case there is a dual description: by a continuous in time Liouville equation that describes time evolution of statistical states, and by the PDP Algorithm that simulates Nature's event generation for individual systems. In the relativistic case we have restricted ourselves to the individual description. In fact, at present, we do not know what would be the right mathematical formalism and its physical interpretation for a relativistic analogue of the Liouville equation. Formally we can write an equation as in the nonrelativistic case, but now using an indefinite metric space. Some of the relevant mathematics have been developed in the past by one of us [33]. What is yet to be done is to study the nonrelativistic limit of the Relativistic PDP and to see that Nonrelativistic PDP of EEQT is recovered this way. The ideas given in the papers by Horwitz [34] and Horwitz and Rotbart [35] can be applied for studying such a limit. Other problems that are yet to be investigated are: quantum field theoretical generalization along the lines of Ref. [13], and an explicit formula for time-of-click probability for a pointlike detector and a special intitial wave packet - as in Ref. [16]. It is to be observed that a quantum field theoretical version will have to involve, as it was for one particle, indefinite metric.

It must be noted that the Relativistic PDP, in cases of more than one detector, involves non-local decision making algorithm. Thus, even if the detectors are treated as classical in our approach, nevertheless there is no local explanation for their behavior. To decide which of the two detectors will click at the event time involves a random choice based on probabilities that are computed non-locally. How Nature herself is doing this - is a big puzzle. A solution to this puzzle must be postponed till a later time when the very nature and origin of the Planck constant, of space and of time are better understood.

Acknowledgment(s)

One of us (A.J.) would like to thank the A. von Humboldt Foundation for support. He would also like to thank Larry Horwitz for encouragement and discussion, and Laura Knight for reading the manuscript.

Bibliography

1
Wheeler, J.A.: ``Delayed-Choice Experiments and Bohr's Elementary Quantum Phenomenon", in Proc. Int. Symp. Found. of Quantum Mechanics, Tokyo 1983, pp. 140-152

2
Bell, J.: ``Towards an exact quantum mechanics", in Themes in Contemporary Physics II. Essays in honor of Julian Schwinger's 70th birthday, Deser, S., and Finkelstein, R. J., Ed., World Scientific, Singapore 1989

3
Bell, J.: ``Against measurement", in Sixty-Two Years of Uncertainty. Historical, Philosophical and Physical Inquiries into the Foundations of Quantum Mechanics, Proceedings of a NATO Advanced Study Institute, August 5-15, Erice, Ed. Arthur I. Miller, NATO ASI Series B vol. 226 , Plenum Press, New York 1990

4
Bell, J: ``Are there quantum jumps?" in Schrödinger, Centenary of a Polymath, Cambridge University Press (1987).

5
Bell, J.S.: ``Beables for quantum field theory", Paper no. 19 in Speakable and unspeakable in quantum mechanics, Cambridge University Press, Cambridge 1987

6
DeWitt, B., Ed.: ``The many-worlds interpretation of quantum mechanics", Princeton Univ. Press, Princeton 1973

7
Blanchard, Ph., and Jadczyk, A.: ``Event-Enhanced-Quantum Theory and Piecewise Deterministic Dynamics", Ann. der Physik 4 (1995) 583-599

8
Primas, H.
Chemistry, Quantum Mechanics and Reductionism: Perspectives in Theoretical Chemistry,
Springer Verlag, Berlin 1981

9
Primas, H.,
The Measurement Process in the Individual Interpretation of Quantum Mechanics,
in The Measurement Problem of Quantum Theory,
Ed. M. Cini and J.M. Lévy-Leblond, IOP Publ. Ldt. Bristol, 1990

10
Amman, A.: ``Broken symmetries and the generation of classical observables in large systems", Helv. Phys. Acta 60 (1987), 384-393

11
Amman, A.: ``Chirality: A superselection rule generated by the molecular environment", J. Molec. Chem. 6 (1991), 1-15

12
Jadczyk, A.: ``Particle Tracks, Events and Quantum Theory", Progr. Theor. Phys. 93 (1995), 631-646

13
Jadczyk, A.: ``On Quantum Jumps, Events and Spontaneous Localization Models", Found. Phys. 25 (1995), 743-762

14
Aharonov, A., and Albert, D.Z.: ``States and observables in relativistic quantum field theories", Phys. Rev. D21 (1980), 3316-3324

15
Peres, A.: ``Relativistic Quantum Measurements", in: Fundamental Problems of Quantum Theory, Ann. NY. Acad. Sci. 755 (1995)

16
Blanchard, Ph., and Jadczyk, A.: ``Time of Events in Quantum Theory", Preprint BiBoS 720/1/96, e-Print Archive: quant-ph/9602010, to appear in Helv. Phys. Acta

17
Blanchard, Ph., and Jadczyk, A.: ``Events and Piecewise Deterministic Dynamics in Event-Enhanced Quantum Theory", Phys. Lett. A203 (1995), 260-266

18
Stapp, H.P.: Mind, Matter and Quantum Mechanics, Springer Verlag, Berlin 1993

19
Stapp, H.P.: ``The Integration of Mind into Physics", in opus cited under [15]

20
Jadczyk, A., Kondrat, G., and Olkiewicz, R.: ``On uniqueness of the jump process in quantum measurement theory", Preprint BiBoS 711/12/95, quant-ph/9512002, submitted to J. Phys. A.

21
Horwitz, L.P., and Piron, C.: ``Relativistic Dynamics", Helv. Phys. Acta 46 (1973), 316-326

22
Kyprianidis, A.: ``Scalar Time Parametrization of Relativistic Quantum Mechanics: the Covariant Schrödinger Formalism", Phys. Rep. 155 (1987), 1-27

23
Fanchi, J.R.: ``Review of Invariant Time Formulations of Relativistic Quantum Theories", Found. Phys. 23 (1993), 487-548

24
Fanchi, J.R.: ``Evaluating the Validity of Parametrized Relativistic Wave Equations", Found. Phys. 24 (1994), 543-562

25
Evans, A.B.: ``Four-Space Formulation of Dirac's Equation", Found. Phys. 20 (1990), 309-335

26
Horwitz, L.P., Piron, C., and Reuse, F.: ``Relativistic Dynamics for the Spin 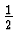$1\over2$ Particle", Helv. Phys. Acta 48 (1975), 546-547

27
Piron, C., and Reuse, F.: ``Relativistic Dynamics for the Spin 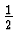$1\over2$ Particle", Helv. Phys. Acta 51 (1978), 146-166

28
Reuse, F.: ``On Classical and Quantum Relativistic Dynamics", Found. Phys. 9 (1979), 865-882

29
Arensburg, A., and Horwitz, L.P.: ``A First-Order Equation for Spin in a Manifestly Relativistically Covariant Quantum Theory", Found. Phys. 22 (1992), 1025-1039

30
Horwitz, L.P., and Arshansky, R.: ``On relativistic quantum theory for particles with spin 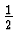$1\over2$", J. Phys. A 15 (1982), L659-L662

31
Jadczyk, A.: ``Topics in Quantum Dynamics", in Proc. First Caribb. School of Math. and Theor. Phys., Saint-Francois-Guadeloupe 1993, Infinite Dimensional Geometry, Noncommutative Geometry, Operator Algebras and Fundamental Interactions, ed. R.Coquereaux et al., World Scientific, Singapore 1995, hep-th 9406204

32
Arshansky, L., Horwitz, L.P., and Lavie, Y.: ``Particles vs. Events: The Concatenated Structure of World Lines in Relativistic Quantum Mechanics", Found. Phys. 13 (1983), 1167-1194

33
Jadczyk, A.: ``Geometry of Indefinite Metric Spaces", Rep. Math. Phys. 2 (1971), 263-276

34
Horwitz, L.P.: ``On the Definition and Evolution of States in Relativistic Classical and Quantum Mechanics", Found. Phys. 22 (1992), 421-448

35
Horwitz, L.P., and Rotbart, F.C.: ``Nonrelativistic limit of relativistic quantum mechanics", Phys. Rev. D 24 (1981), 2127-2131

Footnotes

...${}^\sharp$ 1
e-mail: ajad@ift.uni.wroc.pl
... systems. 2
Necessity of such a coupling was envisaged already in the works by H. Primas [8,9] and A. Amman [10,11].
...blaja95a 3
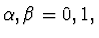
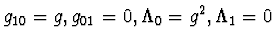
Using the notation of Ref. [7] we put $\alpha,\beta=0,1,$ $g_{10}=g, g_{01}=0, \Lambda_0=g^2, \Lambda_1=0$
... position. 4
Notice that here, as in the nonrelativistic case, we assume that 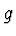$g$ depends only on 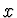$x$ and not on 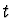$t$ - in the coordinate system with respect the detector is at rest.